题目内容
【题目】设n 为不小于3的正整数,集合![]() ,对于集合
,对于集合![]() 中的任意元素
中的任意元素![]() ,
,![]() 记
记![]()
(Ⅰ)当![]() 时,若
时,若![]() ,请写出满足
,请写出满足![]() 的所有元素
的所有元素![]()
(Ⅱ)设![]() 且
且![]() ,求
,求![]() 的最大值和最小值;
的最大值和最小值;
(Ⅲ)设S是![]() 的子集,且满足:对于S中的任意两个不同元素
的子集,且满足:对于S中的任意两个不同元素![]() ,有
,有![]() 成立,求集合S中元素个数的最大值.
成立,求集合S中元素个数的最大值.
【答案】(1)![]() ; (2)
; (2)![]() 的最大值为
的最大值为![]() ,当
,当![]() 为偶数时,
为偶数时,![]() 的最小值为
的最小值为![]() ,当
,当![]() 为奇数时,
为奇数时,![]() ; (3)
; (3)![]() 中的元素个数最大值为
中的元素个数最大值为![]() .
.
【解析】
(Ⅰ)结合题意列举可得;(Ⅱ)先根据![]() ,得到
,得到![]() 的关系式,再求解
的关系式,再求解![]() 的最值;(Ⅲ)通过对集合
的最值;(Ⅲ)通过对集合![]() 的拆分,逐一求解.
的拆分,逐一求解.
(Ⅰ)满足![]() 的元素为
的元素为![]()
(Ⅱ)记![]() ,
,![]() ,
,
注意到![]() ,所以
,所以![]() ,
,
所以![]()
![]()
![]()
因为![]() ,所以
,所以![]()
所以![]() 中有
中有![]() 个量的值为1,
个量的值为1,![]() 个量的值为0.
个量的值为0.
显然![]()
![]() ,
,
当![]() ,
,![]() 时,
时,
![]() 满足
满足![]() ,
,![]() .所以
.所以![]() 的最大值为
的最大值为![]()
又![]()
![]()
注意到只有![]() 时,
时,![]() ,否则
,否则![]()
而![]() 中
中![]() 个量的值为1,
个量的值为1,![]() 个量的值为0
个量的值为0
所以满足![]() 这样的元素
这样的元素![]() 至多有
至多有![]() 个,
个,
当![]() 为偶数时,
为偶数时,![]() .
.
当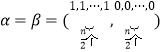 时,满足
时,满足![]() ,且
,且![]() .
.
所以![]() 的最小值为
的最小值为![]()
当![]() 为奇数时,且
为奇数时,且![]() ,这样的元素
,这样的元素![]() 至多有
至多有![]() 个,
个,
所以![]() .
.
当 ,
, 时,满足
时,满足![]() ,
,![]() .
.
所以![]() 的最小值为
的最小值为![]()
综上:![]() 的最大值为
的最大值为![]() ,当
,当![]() 为偶数时,
为偶数时,![]() 的最小值为
的最小值为![]() ,当
,当![]() 为奇数时,
为奇数时,![]() .
.
(Ⅲ)![]() 中的元素个数最大值为
中的元素个数最大值为![]()
设集合![]() 是满足条件的集合中元素个数最多的一个
是满足条件的集合中元素个数最多的一个
记![]()
![]() ,
,
![]()
显然![]()
集合![]() 中元素个数不超过
中元素个数不超过![]() 个,下面我们证明集合
个,下面我们证明集合![]() 中元素个数不超过
中元素个数不超过![]() 个
个
![]() ,则
,则![]()
则![]() 中至少存在两个元素
中至少存在两个元素![]()
![]() ,
,![]()
因为![]() ,所以
,所以![]() 不能同时为
不能同时为![]()
所以对![]() 中的一组数
中的一组数![]() 而言,
而言,
在集合![]() 中至多有一个元素
中至多有一个元素![]() 满足
满足![]() 同时为
同时为![]()
所以集合![]() 中元素个数不超过
中元素个数不超过![]() 个
个
所以集合![]() 中的元素个数为至多为
中的元素个数为至多为![]()
![]() .
.
记![]()
![]() ,则
,则![]() 中共
中共![]() 个元素,
个元素,
对于任意的![]() ,
,![]() ,
,![]() .
.
对![]() ,记
,记![]() 其中
其中![]() ,
,![]() ,
,![]()
记![]() ,
,
显然![]() ,
,![]() ,均有
,均有![]() .
.
记![]() ,
,![]() 中的元素个数为
中的元素个数为![]() ,且满足
,且满足![]() ,
,![]() ,均有
,均有![]() .
.
综上所述,![]() 中的元素个数最大值为
中的元素个数最大值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目