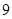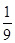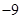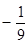题目内容
(本小题满分14分)对定义域分别是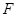 、
、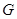 的函数
的函数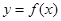 、
、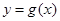 ,
,
规定:函数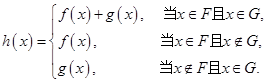
已知函数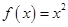 ,
,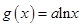
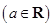 .
.
(1)求函数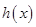 的解析式;
的解析式;
⑵对于实数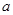 ,函数
,函数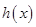 是否存在最小值,如果存在,求出其最小值;如果不存在,请说明理由.
是否存在最小值,如果存在,求出其最小值;如果不存在,请说明理由.
 、
、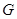 的函数
的函数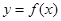 、
、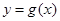 ,
,规定:函数
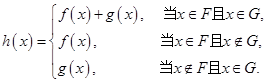
已知函数
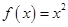 ,
,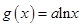
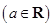 .
.(1)求函数
 的解析式;
的解析式;⑵对于实数
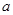 ,函数
,函数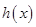 是否存在最小值,如果存在,求出其最小值;如果不存在,请说明理由.
是否存在最小值,如果存在,求出其最小值;如果不存在,请说明理由.(1) ⑵当
⑵当 时,函数
时,函数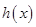 没有最小值;当
没有最小值;当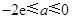 时,函数
时,函数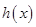 的最小值为
的最小值为 ;当
;当 时,函数
时,函数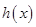 的最小值为
的最小值为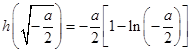
 ⑵当
⑵当 时,函数
时,函数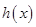 没有最小值;当
没有最小值;当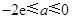 时,函数
时,函数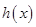 的最小值为
的最小值为 ;当
;当 时,函数
时,函数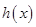 的最小值为
的最小值为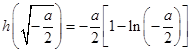
试题分析:(1)因为函数
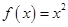 的定义域
的定义域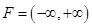 ,函数
,函数 的定义域
的定义域 ,所以
,所以 ………………4分
………………4分(2)当
 时,函数
时,函数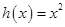 单调递减,
单调递减,所以函数
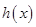 在
在 上的最小值为
上的最小值为 .当
.当 时,
时,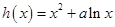 .
.若
 ,函数
,函数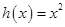 .此时,函数
.此时,函数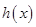 存在最小值h(0)=0.
存在最小值h(0)=0.若
 ,因为
,因为 ,
,所以函数
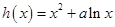 在
在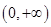 上单调递增.此时,函数
上单调递增.此时,函数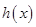 不存在最小值.
不存在最小值.若
 ,因为
,因为 ,
,所以函数
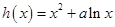 在
在 上单调递减,在
上单调递减,在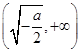 上单调递增.此时,函数
上单调递增.此时,函数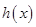 的最小值为
的最小值为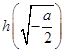 .
.因为
 ,
,所以当
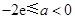 时,
时,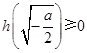 ,当
,当 时,
时,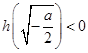 .
.综上可知,当
 时,函数
时,函数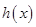 没有最小值;当
没有最小值;当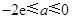 时,函数
时,函数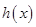 的最小值为
的最小值为 ;当
;当 时,函数
时,函数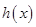 的最小值为
的最小值为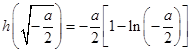 .…………………14分
.…………………14分点评:本题第一小题考查的是分段函数,分段函数针对于不同的自变量的范围有不同的解析式,第二小题难在需要对a分情况讨论从而确定函数单调性求解其最值,学生不易找到分情况讨论的入手点,本题难度大

练习册系列答案
相关题目
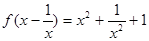 ,则
,则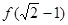 =_ _____
=_ _____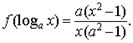
 的表达式,并判断
的表达式,并判断 时,恒有
时,恒有 求m的取值范围。
求m的取值范围。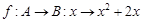 为
为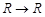 的映射,若对
的映射,若对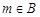 ,在A中无原像,则m取值范围是( )
,在A中无原像,则m取值范围是( )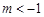

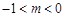
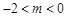
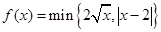 ,其中
,其中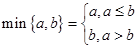 ,若动直线
,若动直线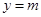 与函数
与函数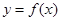 的图像有三个不同的交点,则实数
的图像有三个不同的交点,则实数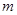 的取值范围是______________.
的取值范围是______________.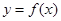 对任意实数
对任意实数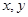 都有
都有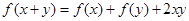 ,
,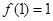
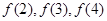 的值;
的值;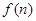
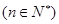 的表达式,并用数学归纳法证明你的结论.
的表达式,并用数学归纳法证明你的结论.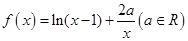 ,
,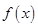 的图像在点
的图像在点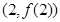 处的切线方程;
处的切线方程;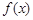 的单调区间;
的单调区间;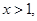 且
且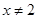 时,
时,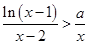 恒成立,求实数
恒成立,求实数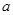 的取值范围。
的取值范围。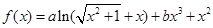 ,其中
,其中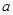 、
、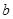 为常数,
为常数,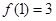 ,则
,则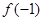 =_________.
=_________.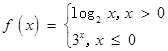 , 则
, 则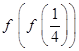 的值是
的值是