题目内容
20.求函数f(x)=x3-x+6在区间[-1,1]上的最大值与最小值.分析 求出f(x)的导数,求得函数的极值点,计算极值,求得端点处的函数值,比较即可得到最值.
解答 解:∵f'(x)=3x2-1,
由f'(x)=0得$x=±\frac{{\sqrt{3}}}{3}$.
| x | -1 | $(-1,-\frac{{\sqrt{3}}}{3})$ | $-\frac{{\sqrt{3}}}{3}$ | $(-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3})$ | $\frac{{\sqrt{3}}}{3}$ | $(\frac{{\sqrt{3}}}{3},1)$ | 1 |
| f'(x) | + | 0 | - | 0 | + | ||
| f(x) | 6 | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 | 6 |
比较$x=-\frac{{\sqrt{3}}}{3}$、$x=\frac{{\sqrt{3}}}{3}$、x=-1和x=1的函数值f(-1)=6,f(1)=6,
$f(-\frac{{\sqrt{3}}}{3})=6+\frac{{2\sqrt{3}}}{9}$,$f(\frac{{\sqrt{3}}}{3})=6-\frac{{2\sqrt{3}}}{9}$的大小可得:
函数f(x)在区间[-1,1]上的最大值是$6+\frac{{2\sqrt{3}}}{9}$,最小值是$6-\frac{{2\sqrt{3}}}{9}$.
点评 本题考查导数的运用:求单调区间、极值和最值,主要考查二次不等式的解法,以及函数值大小的比较,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
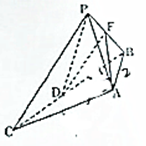 如图,在三棱锥P-ABC中,D是线段BC的中点,△ABC和△PAD所在的平面互相垂直,PA⊥AD,AF⊥PB,AB=2,AC=4,AD=$\sqrt{3}$,∠BAC=120°.
如图,在三棱锥P-ABC中,D是线段BC的中点,△ABC和△PAD所在的平面互相垂直,PA⊥AD,AF⊥PB,AB=2,AC=4,AD=$\sqrt{3}$,∠BAC=120°.