题目内容
已知函数 .(
.( 为常数)
为常数)
(1)当 时,求函数
时,求函数 的最小值;
的最小值;
(2)求函数 在
在 上的最值;
上的最值;
(3)试证明对任意的 都有
都有
【答案】
解(1)当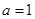 时,函数
时,函数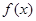 =
=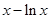
 ,
,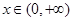
∵ ,令
,令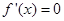 得
得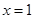
∵当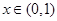 时,
时,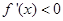 ∴函数
∴函数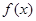 在
在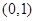 上为减函数
上为减函数
∵当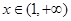 时
时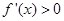 ∴函数
∴函数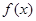 在
在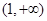 上为增函数
上为增函数
∴当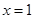 时,函数
时,函数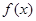 有最小值,
有最小值,
(2)∵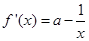
若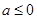 ,则对任意的
,则对任意的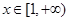 都有
都有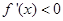 ,∴函数
,∴函数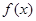 在
在 上为减函数
上为减函数
∴函数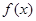 在
在 上有最大值,没有最小值,
上有最大值,没有最小值,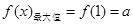 ;
;
若 ,令
,令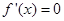 得
得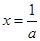
当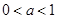 时,
时,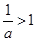 ,当
,当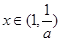 时
时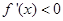 ,函数
,函数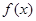 在
在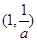 上为减函数
上为减函数
当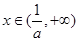 时
时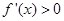 ∴函数
∴函数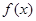 在
在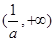 上为增函数
上为增函数
∴当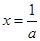 时,函数
时,函数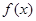 有最小值,
有最小值,
当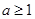 时,
时,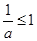 在
在 恒有
恒有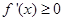
∴函数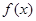 在
在 上为增函数,
上为增函数,
函数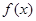 在
在 有最小值,
有最小值,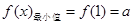 .
.
综上得:当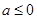 时,函数
时,函数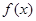 在
在 上有最大值,
上有最大值,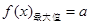 ,没有最小值;
,没有最小值;
当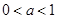 时,函数
时,函数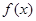 有最小值,
有最小值,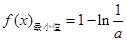 ,没有最大值;
,没有最大值;
当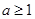 时,函数
时,函数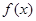 在
在 有最小值,
有最小值, ,没有最大值.
,没有最大值.
(3)由(1)知函数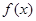 =
=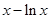 在
在 上有最小值1
上有最小值1
即对任意的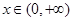 都有
都有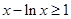 ,即
,即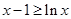 ,
,
当且仅当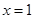 时“=”成立
时“=”成立
∵ ∴
∴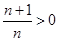 且
且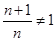
∴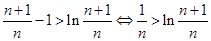
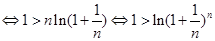
∴对任意的 都有
都有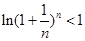 .
.
【解析】略

练习册系列答案
相关题目































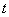




 (
( 为常数,
为常数, 且
且 )的图象过点
)的图象过点 .
. ,试判断函数
,试判断函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.  (
( 为常数,
为常数, ),满足
),满足 ,且
,且 有两个相同的解。
有两个相同的解。 的表达式;
的表达式; 满足
满足 ,且
,且 ,求证:数列
,求证:数列 是等差数列。
是等差数列。 (
( 为常数),直线l与函数
为常数),直线l与函数 的图象都相切,且l与函数
的图象都相切,且l与函数 的图象的切点的横坐标为l.
的图象的切点的横坐标为l. 的解的个数.
的解的个数.