题目内容
已知函数 (
( 为常数,且
为常数,且 ).
).
(1)当 时,求函数
时,求函数 的最小值(用
的最小值(用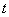 表示);
表示);
(2)是否存在不同的实数 使得
使得 ,
, ,并且
,并且 ,若存在,求出实数
,若存在,求出实数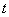 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】
(1)函数 的最小值为
的最小值为 ;
;
(2)满足条件的 存在,取值范围为
存在,取值范围为 .
.
【解析】
试题分析:(1)构造新函数 ,分
,分 和
和 两种情况讨论即可;(2)假设存在,则由已知得
两种情况讨论即可;(2)假设存在,则由已知得  ,等价于
,等价于 在区间
在区间 上有两个不同的实根,作出函数图象,可得
上有两个不同的实根,作出函数图象,可得 .
.

试题解析:(1)令 1分
1分
当 即
即 时,
时,  4分
4分
当 即
即 时,
时, 7分
7分
综上: . 8分
. 8分
(2)解法一:假设存在,则由已知得
 ,等价于
,等价于 在区间
在区间 上有两个不同的实根 11分
上有两个不同的实根 11分
令 ,则
,则 在
在 上有两个不同的零点
上有两个不同的零点
 . 15分
. 15分
解法2:假设存在,则由已知得

等价于 在区间
在区间 上有两个不同的实根 11分
上有两个不同的实根 11分
等价于 ,作出函数图象,可得
,作出函数图象,可得 . 15分
. 15分
考点:函数的最值、分类讨论思想、数形结合思想.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
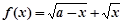 (
(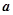 为常数,且
为常数,且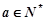 ),对于定义域内的任意两个实数
),对于定义域内的任意两个实数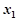 、
、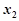 ,恒有
,恒有 成立,则正整数
成立,则正整数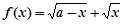 (
(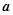 为常数,且
为常数,且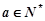 ),对于定义域内的任意两个实数
),对于定义域内的任意两个实数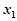 、
、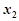 ,恒有
,恒有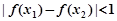 成立,则正整数
成立,则正整数 (
(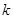 为常数,
为常数, 且
且 ),且数列
),且数列 是首项为4,
是首项为4, 是等比数列;
是等比数列; ,当
,当 时,求数列
时,求数列 的前
的前 项和
项和 ;
; ,且
,且 与
与 的大小.
的大小.