题目内容
已知函数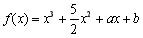 (
(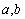 为常数),其图象是曲线
为常数),其图象是曲线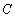 .
.
(1)当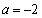 时,求函数
时,求函数 的单调减区间;
的单调减区间;
(2)设函数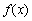 的导函数为
的导函数为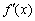 ,若存在唯一的实数
,若存在唯一的实数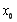 ,使得
,使得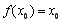 与
与 同时成立,求实数
同时成立,求实数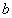 的取值范围;
的取值范围;
(3)已知点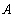 为曲线
为曲线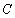 上的动点,在点
上的动点,在点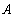 处作曲线
处作曲线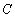 的切线
的切线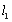 与曲线
与曲线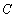 交于另一点
交于另一点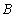 ,在点
,在点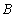 处作曲线
处作曲线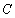 的切线
的切线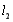 ,设切线
,设切线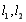 的斜率分别为
的斜率分别为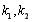 .问:是否存在常数
.问:是否存在常数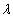 ,使得
,使得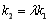 ?若存在,求出
?若存在,求出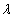 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】
(1)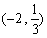 ;(2)
;(2)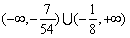 ;(3)当
;(3)当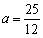 时,存在常数
时,存在常数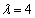 ,使
,使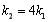 ;当
;当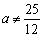 时,不存在常数
时,不存在常数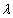 ,使
,使 .
.
【解析】
试题分析:(1)这是一个求函数单调递减区间的问题,比较简单,可以通过导数的符号去判断;(2)这是一个两方程有公共解且公共解唯一的问题,消去参数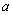 后就转化为含有参数
后就转化为含有参数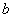 的关于未知数
的关于未知数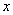 的三次方程有唯一解的问题,可利用三次函数的图象判断;(3)可设
的三次方程有唯一解的问题,可利用三次函数的图象判断;(3)可设 ,然后把点
,然后把点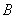 的坐标和
的坐标和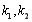 都用
都用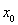 表示,再考察关于
表示,再考察关于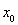 的等式
的等式 恒成立,从而去确定常数
恒成立,从而去确定常数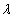 是否存在.
是否存在.
试题解析:(1)当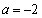 时,
时, 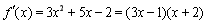 . 2分
. 2分
令f ?(x)<0,解得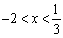 ,f(x)的单调减区间为
,f(x)的单调减区间为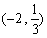 . 4分
. 4分
(2) 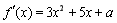 ,
,
由题意知 消去
消去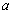 ,得
,得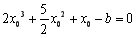 有唯一解. 6分
有唯一解. 6分
令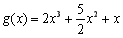 ,则
,则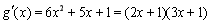 ,
,
以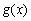 在区间
在区间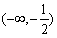 ,
,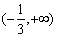 上是增函数,在
上是增函数,在 上是减函数, 8分
上是减函数, 8分
又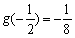 ,
,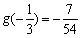 ,
,
故实数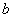 的取值范围是
的取值范围是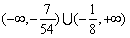 . 10分
. 10分
(3) 设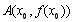 ,则点
,则点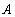 处切线方程为
处切线方程为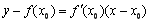 ,
,
与曲线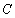 :
: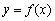 联立方程组,得
联立方程组,得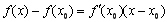 ,即
,即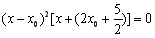 ,所以
,所以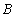 点的横坐标
点的横坐标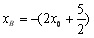 . 12分
. 12分
由题意知, ,
, ,
,
若存在常数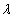 ,使得
,使得 ,则
,则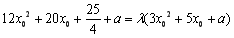 ,
,
即常数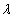 ,使得
,使得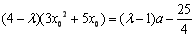 ,
,
所以常数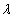 ,使得
,使得 解得常数
解得常数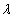 ,使得
,使得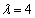 ,
,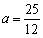 . 15分
. 15分
故当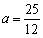 时,存在常数
时,存在常数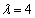 ,使
,使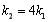 ;当
;当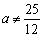 时,不存在常数
时,不存在常数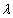 ,使
,使 .16分
.16分
考点:函数与方程、导数的综合应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
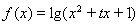
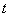
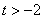
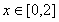
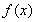

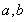
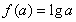
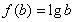
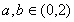
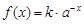 (
(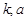 为常数,
为常数, 且
且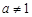 )的图象过点
)的图象过点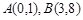 .
.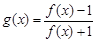 ,试判断函数
,试判断函数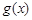 的奇偶性,并说明理由.
的奇偶性,并说明理由. 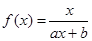 (
(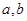 为常数,
为常数,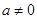 ),满足
),满足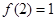 ,且
,且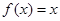 有两个相同的解。
有两个相同的解。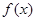 的表达式;
的表达式;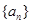 满足
满足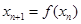 ,且
,且 ,求证:数列
,求证:数列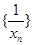 是等差数列。
是等差数列。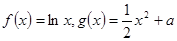 (
( 为常数),直线l与函数
为常数),直线l与函数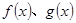 的图象都相切,且l与函数
的图象都相切,且l与函数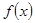 的图象的切点的横坐标为l.
的图象的切点的横坐标为l.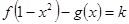 的解的个数.
的解的个数.