题目内容
11.在△ABC中,内角A,B,C对应边分别是a,b,c,若bcosC+ccosB=asinA,则△ABC的形状是( )三角形.| A. | 直角 | B. | 锐角 | C. | 钝角 | D. | 任意 |
分析 依题意,利用正弦定理和两角和的正弦公式,可知sin(B+C)=sinA=sin2A,易求sinA=1,从而可得答案.
解答 解:△ABC中,∵bcosC+ccosB=asinA,
∴由正弦定理得:sinBcosC+sinCcosB=sin2A,
即sin(B+C)=sin(π-A)=sinA=sin2A,又sinA>0,
∴sinA=1,A∈(0,π),
∴A=$\frac{π}{2}$.
∴△ABC的形状是直角三角形,
故选:A.
点评 本题考查三角形形状的判断,着重考查正弦定理与诱导公式,两角和的正弦公式的应用,考查转化思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.在曲线y=x2(x≥0)上某一点A处作一切线使之与曲线以及x轴所围的面积为$\frac{1}{12}$,则这个切线方程是.( )
| A. | y=-2x-1 | B. | y=-2x+1 | C. | y=2x-1 | D. | y=2x+1 |
19.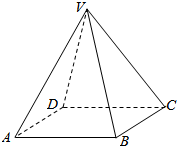 如图,已知四棱锥 V-ABCD的底面是边长为2正方形,侧面都是侧棱长为$\sqrt{5}$的等腰三角形,则二面角V-AB-C的大小为( )
如图,已知四棱锥 V-ABCD的底面是边长为2正方形,侧面都是侧棱长为$\sqrt{5}$的等腰三角形,则二面角V-AB-C的大小为( )
 如图,已知四棱锥 V-ABCD的底面是边长为2正方形,侧面都是侧棱长为$\sqrt{5}$的等腰三角形,则二面角V-AB-C的大小为( )
如图,已知四棱锥 V-ABCD的底面是边长为2正方形,侧面都是侧棱长为$\sqrt{5}$的等腰三角形,则二面角V-AB-C的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
3.在△ABC中,若BC=3,AC=4,AB=$\sqrt{13}$,则△ABC的面积等于( )
| A. | 3$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 10$\sqrt{3}$ |
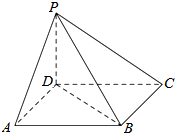 如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2PD=4,PD⊥底面ABCD.
如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2PD=4,PD⊥底面ABCD.