题目内容
6.设曲线f(x)=ax+ex在点(0,1)处的切线与直线x+y-1=0垂直,则实数a=0.分析 求出导数,求得切线的斜率,由两直线垂直的条件:斜率之积为-1,解方程可得a=0.
解答 解:f(x)=ax+ex的导数为f′(x)=a+ex,
在点(0,1)处的切线斜率为k=a+1,
由切线与直线x+y-1=0垂直,可得
a+1=1,解得a=0.
故答案为:0.
点评 本题考查导数的运用:求切线的斜率,考查两直线垂直的条件:斜率之积为-1,正确求导是解题的关键.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
1.若f(x)是定义在R上的偶函数,且当x<0时,f(x)=x+2,则f(1)的值为( )
| A. | 1 | B. | -1 | C. | -3 | D. | 3 |
15.若2a=4,则loga$\frac{1}{2}$的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | $\frac{1}{2}$ |
16.下列函数中,能用二分法求零点的是( )
| A. | f(x)=log2x | B. | f(x)=-x2 | C. | f(x)=x2 | D. | f(x)=|x| |
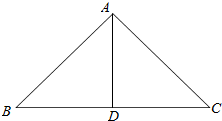 如图:已知△ABC中,∠BAD=∠C,AB=4,BD=2,$\overrightarrow{BD}$=$\overrightarrow{m}$.
如图:已知△ABC中,∠BAD=∠C,AB=4,BD=2,$\overrightarrow{BD}$=$\overrightarrow{m}$.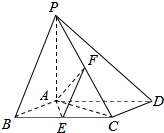 如图,已知四棱锥P-ABCD,底面ABCD为边长为2对的菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为边长为2对的菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.