题目内容
14.已知$\overrightarrow m=(2cosx,1)$,$\overrightarrow n=(cosx,sin2x+a)$,$f(x)=\overrightarrow m•\overrightarrow n$.(Ⅰ)求函数f(x)的最小正周期和单调递增区间;
(Ⅱ)当$x∈[0,\frac{3π}{8}]$时,f(x)的最大值为$\sqrt{2}$,且在此范围内,关于x的方程f(x)=k恰有2个解,确定a的值,并求k的范围.
分析 (1)运用数量积的坐标计算公式,辅助角公式化简函数式,再求最小正周期和单调区间;
(2)根据自变量的范围得出函数的最值,求出a,再结合函数图象求k的范围.
解答 解:(1)f(x)=2cos2x+sin2x+a
=cos2x+sin2x+a+1=$\sqrt{2}$sin(2x+$\frac{π}{4}$)+a+1,
该函数的最小正周期为:π,
令2x+$\frac{π}{4}$∈[2kπ-$\frac{π}{2}$,2kπ+$\frac{π}{2}$],解得x∈[kπ-$\frac{3π}{8}$,kπ+$\frac{π}{8}$];
所以,f(x)的单调增区间为[kπ-$\frac{3π}{8}$,kπ+$\frac{π}{8}$](k∈Z);
(2)当x∈[0,$\frac{3π}{8}$]时,2x+$\frac{π}{4}$∈[$\frac{π}{4}$,π],
此时,sin(2x+$\frac{π}{4}$)∈[0,1],
所以,f(x)max=$\sqrt{2}$+a+1=$\sqrt{2}$,解得a=-1,
因此,f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),
要使f(x)=k在x∈[0,$\frac{3π}{8}$]内恰有两解,
结合正弦函数图象知,k∈[f(0),f($\frac{π}{8}$)),即k∈[1,$\sqrt{2}$),
故实数k的取值范围为[1,$\sqrt{2}$).
点评 本题主要考查了向量的数量积,三角函数恒等变换,三角函数的图象与性质,以及运用函数图象解决根的个数问题,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.函数$y=2sin(2ωx-\frac{π}{3})$周期是π,则ω2等于( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | 4 | D. | 2 |
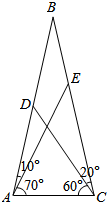 如图,已知∠DAE=10°,∠CAE=70°,∠DCA=60°,∠DCE=20°,则∠DEA=20°.
如图,已知∠DAE=10°,∠CAE=70°,∠DCA=60°,∠DCE=20°,则∠DEA=20°.
 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周四尺,高三尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图),米堆底部的弧长为4尺,米堆的高为3尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周四尺,高三尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图),米堆底部的弧长为4尺,米堆的高为3尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有( )