题目内容
已知函数 ,
, 的最大值为2.
的最大值为2.
(1)求函数 在
在 上的值域;
上的值域;
(2)已知 外接圆半径
外接圆半径 ,
, ,角
,角 所对的边分别是
所对的边分别是 ,求
,求 的值.
的值.
(1)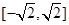 ;(2)
;(2)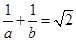 .
.
解析试题分析:本题主要考查三角函数的最值问题、函数的单调性、正弦定理等基础知识,同时考查运算转化能力和计算能力.第一问,利用最大值为 ,可以解出m的值,利用两角和的正弦公式化简
,可以解出m的值,利用两角和的正弦公式化简 ,根据函数定义域求
,根据函数定义域求 的值域;第二问,利用第一问
的值域;第二问,利用第一问 的表达式,化简
的表达式,化简 ,再利用正弦定理将角转化成边,由
,再利用正弦定理将角转化成边,由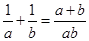 ,从而得到
,从而得到 的值.
的值.
试题解析:(1)由题意, 的最大值为
的最大值为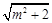 ,所以
,所以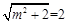 . 2分
. 2分
而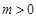 ,于是
,于是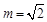 ,
,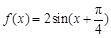 . 4分
. 4分
在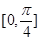 上递增.在
上递增.在 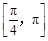 递减,
递减,
所以函数 在
在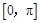 上的值域为
上的值域为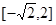 ; 5分
; 5分
(2)化简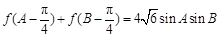
得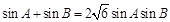 . 7分
. 7分
由正弦定理,得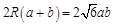 , 9分
, 9分
因为△ABC的外接圆半径为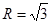 .
. . 11分
. 11分
所以  12分
12分
考点:1.两角和的正弦公式;2.正弦定理;3.三角函数值域.

练习册系列答案
相关题目
 求边C及面积S
求边C及面积S .
. ,b=5,求向量
,b=5,求向量 在
在 方向上的投影.
方向上的投影. -1)海里的C处的缉私船奉命以10
-1)海里的C处的缉私船奉命以10
 asinC-b-c=0.
asinC-b-c=0. asinC-ccosA.
asinC-ccosA. ,1),n="(-2,cos" 2A+1),且m⊥n.
,1),n="(-2,cos" 2A+1),且m⊥n. ,且△ABC的面积S=
,且△ABC的面积S= 时,求边c的值和△ABC的面积.
时,求边c的值和△ABC的面积. ,∠B=2∠A.
,∠B=2∠A.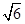 ,∠B=2∠A.
,∠B=2∠A.