题目内容
15.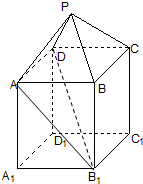 (理科)如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥.AB=4,BC=3,点P∈平面CC1D1D且PD=PC=2$\sqrt{2}$.
(理科)如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥.AB=4,BC=3,点P∈平面CC1D1D且PD=PC=2$\sqrt{2}$.(Ⅰ)证明:PD⊥平面PBC;
(Ⅱ)求PA与平面ABCD所成的角的正切值;
(Ⅲ)若AA1=t,当t为何值时,PC∥平面AB1D.
分析 (Ⅰ)由已知易得△PCD为等腰直角三角形,PD⊥PC,BC⊥面CC1DD1,可求BC⊥PD,从而可证得PD⊥平面PBC.
(Ⅱ)过P点在平面CC1DD作PE⊥CD于E,连接AE,可得PE⊥面ABCD,∠PAE就是PA与平面ABCD所成的角,利用tan∠PAE=$\frac{PE}{AE}$即可得解.
(Ⅲ)当t=4时,四边形面CC1DD1是一个正方形,可求∠PDC=45°,C1D⊥PD.又PC∥C1D.可证PC∥面AB1C1D,从而得证.
解答 解:(Ⅰ)证明:因为PD=PC=2$\sqrt{2}$,CD=AB=4,
所以△PCD为等腰直角三角形,
所以PD⊥PC.(1分)
因为ABCD-A1B1C1D1是一个长方体,所以BC⊥面CC1DD1,(2分)
而P∈面CC1DD1,所以PD?面CC1DD1,所以BC⊥PD.(3分)
因为PD垂直于平面PBC内的两条相交直线PC和BC,(4分)
(或PC∩BC=C也可)
由线面垂直的判定定理,(不说也可)
可得PD⊥平面PBC.
(Ⅱ)过P点在平面CC1DD作PE⊥CD于E,连接AE. (6分)
因为面ABCD⊥面PCD,所以PE⊥面ABCD,(7分)
所以∠PAE就是PA与平面ABCD所成的角 (8分)
因为PE=2,AE=$\sqrt{13}$,所以tan∠PAE=$\frac{PE}{AE}=\frac{2}{\sqrt{13}}=\frac{2\sqrt{13}}{13}$. (9分)
所以PA与平面ABCD所成的角的正切值为$\frac{2\sqrt{13}}{13}$. (10分)
(Ⅲ)当t=4时,PC∥平面AB1D. (11分)
当t=4时,四边形面CC1DD1是一个正方形,所以∠C1DC=45°,而∠PDC=45°,
所以∠PDC1=90°,所以C1D⊥PD. (12分)
而PC⊥PD,C1D与PC在同一个平面内,所以PC∥C1D. (13分)
而C1D?平面AB1C1D,所以PC∥面AB1C1D,所以PC∥平面AB1D. (14分)
点评 本题主要考查了直线与平面垂直的判定,直线与平面平行的判定,直线与平面所成的角的求法,考查了空间想象能力和推理论证能力,属于基本知识的考查.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案| A. | 2 | B. | $\frac{15}{4}$ | C. | $\frac{17}{4}$ | D. | $\frac{3}{2}$ |
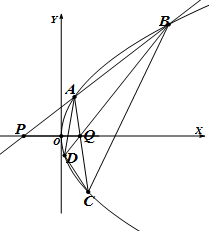 已知抛物线Γ:y2=2px,准线与x轴的交点为P(-2,0).
已知抛物线Γ:y2=2px,准线与x轴的交点为P(-2,0).