题目内容
19.设Sn为数列{an}的前n项和,且a1=1,nan+1=(n+2)Sn+n(n+1),n∈N*.(Ⅰ)证明:数列{${\frac{S_n}{n}$+1}为等比数列;
(Ⅱ)求 Tn=S1+S2+…+Sn.
分析 (Ⅰ)由nan+1=(n+2)Sn+n(n+1),得n(Sn+1-Sn)=(n+2)Sn+n(n+1),变形可得$\frac{{S}_{n+1}}{n+1}$+1=2($\frac{Sn}{n}$+1),即数列{$\frac{Sn}{n}$+1}为等比数列;
(Ⅱ)由(Ⅰ)求得Sn=n•2n-n,然后利用数列的分组求和及错位相减法求和得答案.
解答 (Ⅰ)证明:∵an+1=Sn+1-Sn,由nan+1=(n+2)Sn+n(n+1),得n(Sn+1-Sn)=(n+2)Sn+n(n+1),
即nSn+1=2(n+1)Sn+n(n+1),则$\frac{{S}_{n+1}}{n+1}$=2×$\frac{Sn}{n}$+1,
∴$\frac{{S}_{n+1}}{n+1}$+1=2($\frac{Sn}{n}$+1),
故数列{$\frac{Sn}{n}$+1}为等比数列;
(Ⅱ)解:由(Ⅰ)知$\frac{Sn}{n}$+1=($\frac{S1}{1}$+1)•2n-1=2n,
∴Sn=n•2n-n,
则Tn=(1•2+2•22+…+n•2n)-(1+2+…+n),
设M=1•2+2•22+…+n•2n,
则2M=1•22+2•23+…+n•2n+1,
∴-M=2+22+…+2n-n•2n+1=2n+1-2-n•2n+1,
∴M=(n-1)•2n+1+2,
则Tn=(n-1)•2n+1+2-$\frac{n(n+1)}{2}$.
点评 本题考查了等比关系的确定,考查了等比数列的通项公式,训练了错位相减法求数列的和,是中档题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
10.某几何体的三视图如图所示,则该几何体的体积为( )
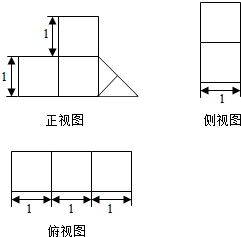

| A. | $\frac{7}{3}$ | B. | $\frac{7}{2}$ | C. | $\frac{9}{2}$ | D. | $\frac{9}{4}$ |
7.设i是虚数单位,复数$\frac{{-2\sqrt{3}+i}}{{1+2\sqrt{3}i}}$=( )
| A. | -1 | B. | 1 | C. | -i | D. | i |
8.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}x,0<x≤2}\\{-|x-3|,x>2}\end{array}\right.$,若方程f(x)=ax+1有三个不同的实数根,则实数a的取值范围是( )
| A. | (-1,-$\frac{1}{3}$) | B. | (-1,-$\frac{1}{3}$] | C. | (-∞,-1)∪[-$\frac{1}{3}$,+∞) | D. | (-∞,-1)∪(-$\frac{1}{3}$,+∞) |