题目内容
定义在(-1,1)上的函数f(x)是减函数,且f(a-1)>f(2a),则a的取值范围是 .(结果用集合或区间表示)
【答案】分析:首先根据函数的定义域为(-1,1)可得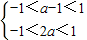 ,进而根据函数的单调性可得a-1<2a,由此构造不等式组,解不等式组可得答案.
,进而根据函数的单调性可得a-1<2a,由此构造不等式组,解不等式组可得答案.
解答:解:若函数f(x)是定义在(-1,1)上的减函数,
则不等式f(a-1)>f(2a),可化为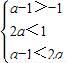
解得0<a<
即a的取值范围是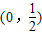
故答案为:
点评:本题考查的知识点是函数的单调性和函数的定义域,其中本题易忽略定义域对a的限制,而错解为(-1,+∞)
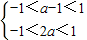 ,进而根据函数的单调性可得a-1<2a,由此构造不等式组,解不等式组可得答案.
,进而根据函数的单调性可得a-1<2a,由此构造不等式组,解不等式组可得答案.解答:解:若函数f(x)是定义在(-1,1)上的减函数,
则不等式f(a-1)>f(2a),可化为
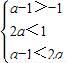
解得0<a<

即a的取值范围是
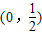
故答案为:

点评:本题考查的知识点是函数的单调性和函数的定义域,其中本题易忽略定义域对a的限制,而错解为(-1,+∞)

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.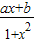 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.