题目内容
已知{an}为等差数列,a1+a3+a5=105,a2+a4+a6=99,以Sn表示数列{an}的前n项和,则使得Sn达到最大值的n是( )
| A.21 | B.20 | C.19 | D.18 |
B
解:设{an}的公差为d,由题意得
a1+a3+a5=a1+a1+2d+a1+4d=105,即a1+2d=35,①
a2+a4+a6=a1+d+a1+3d+a1+5d=99,即a1+3d=33,②
由①②联立得a1=39,d=-2,
∴sn="39n+n(n-1)" 2 ×(-2)=-n2+40n=-(n-20)2+400,
故当n=20时,Sn达到最大值400.
故选B.
a1+a3+a5=a1+a1+2d+a1+4d=105,即a1+2d=35,①
a2+a4+a6=a1+d+a1+3d+a1+5d=99,即a1+3d=33,②
由①②联立得a1=39,d=-2,
∴sn="39n+n(n-1)" 2 ×(-2)=-n2+40n=-(n-20)2+400,
故当n=20时,Sn达到最大值400.
故选B.

练习册系列答案
相关题目
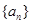 、
、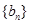 前
前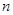 项和分别为
项和分别为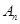 、
、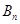 ,满足
,满足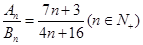 ,
,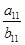 的值为( )
的值为( )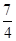
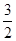
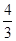
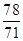
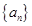 满足:
满足: ,
,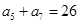 ,
,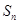 .
.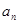 及前n项和
及前n项和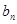 =
=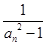 (n
(n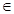 N*),求数列
N*),求数列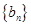 的前n项和
的前n项和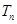 .
.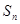 是等差数列
是等差数列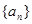 的前n项和,已知
的前n项和,已知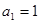 ,公差d=2,则
,公差d=2,则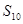 ="_______" .
="_______" .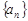 的前
的前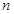 项和为
项和为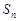 ,
,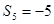 ,
,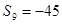 ,则
,则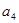 的值为( )
的值为( ) 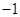
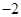
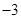
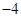
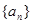 中,若
中,若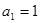 ,
,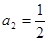 ,
,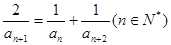 ,则该数列的通项为 .
,则该数列的通项为 . 
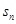 是等差数列{
是等差数列{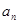 }的前n项和,已知
}的前n项和,已知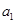 =3,
=3,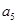 =11,则
=11,则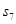 等于_________
等于_________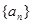 中,
中,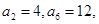 则公差d= ( )
则公差d= ( )