题目内容
已知函数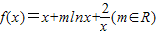
．（I）当m=1时，求f（x）的单调区间；
（Ⅱ）若曲线y=f（x）在点（2，f（x））处的切线与直线y=
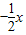平行，求m的值．
【答案】分析：（I）当m=1时，确定函数的定义域，求导函数，利用导数的正负，即可求f（x）的单调区间；
（Ⅱ）求导函数，利用导数的几何意义，建立方程，即可求m的值．
解答：解：（I）函数f（x）的定义域为{x|x＞0}
当m=1时，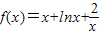
，
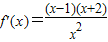
令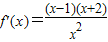
＞0可得x＜-2或x＞1；令
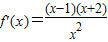＜0，可得-2＜x＜1
∵x＞0，∴，f（x）的单调增区间为（1，+∞），单调减区间为（0，1）；
（Ⅱ）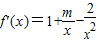
∵曲线y=f（x）在点（2，f（x））处的切线与直线y=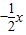
平行，
∴
=-
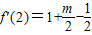∴m=-2．
点评：本题考查导数知识的运用，考查函数的单调性，考查导数的几何意义，考查学生的计算能力，属于中档题．
（Ⅱ）求导函数，利用导数的几何意义，建立方程，即可求m的值．
解答：解：（I）函数f（x）的定义域为{x|x＞0}
当m=1时，
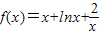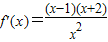
，令
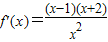＞0可得x＜-2或x＞1；令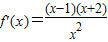＜0，可得-2＜x＜1∵x＞0，∴，f（x）的单调增区间为（1，+∞），单调减区间为（0，1）；
（Ⅱ）
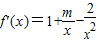
∵曲线y=f（x）在点（2，f（x））处的切线与直线y=
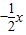平行，∴
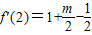=-∴m=-2．
点评：本题考查导数知识的运用，考查函数的单调性，考查导数的几何意义，考查学生的计算能力，属于中档题．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
．
．
．
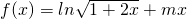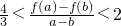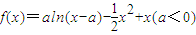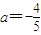时，记函数f（x）的零点为x，若对任意x1，x2∈[0，x]且x2-x1=1，都有|f（x2）-f（x1）|≥m成立，求实数m的最大值．
，
）
．
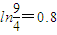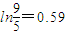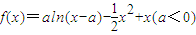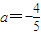时，记函数f（x）的零点为x，若对任意x1，x2∈[0，x]且x2-x1=1，都有|f（x2）-f（x1）|≥m成立，求实数m的最大值．
，
）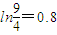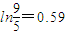