题目内容
已知函数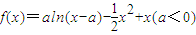 .
.(I)当-1<a<0时,求f(x)的单调区间;
(II)若-1<a<2(ln2-1),求证:函数f(x)只有一个零点x,且a+1<x<a+2;
(III)当
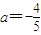 时,记函数f(x)的零点为x,若对任意x1,x2∈[0,x]且x2-x1=1,都有|f(x2)-f(x1)|≥m成立,求实数m的最大值.
时,记函数f(x)的零点为x,若对任意x1,x2∈[0,x]且x2-x1=1,都有|f(x2)-f(x1)|≥m成立,求实数m的最大值.(本题可参考数据:ln2=0.7,
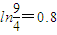 ,
,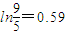 )
)
【答案】分析:(I)f(x)的定义域为(a,+∞).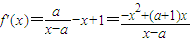 .由此能求出题函数f(x)的单调区间.
.由此能求出题函数f(x)的单调区间.
(II)当-1<a<2(ln2-1)<0时,由(I)知,f(x)的极小值为f(0),极大值为f(a+1).由此能够证明函数f(x)只有一个零点x,且a+1<x<a+2.
(III)因为 ,所以任意x1,x2∈[0,x]且x2-x1=1,由(II)可知x1∈[0,a+1],x2∈(a+1,x],且x2≥1.由此能推导出使得|f(x2)-f(x1)|≥m恒成立的m的最大值.
,所以任意x1,x2∈[0,x]且x2-x1=1,由(II)可知x1∈[0,a+1],x2∈(a+1,x],且x2≥1.由此能推导出使得|f(x2)-f(x1)|≥m恒成立的m的最大值.
解答:(I)解:f(x)的定义域为(a,+∞).
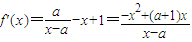 .
.
令f'(x)=0⇒x=0或x=a+1.
当-1<a<0时,a+1>0,函数f(x)与f'(x)随x的变化情况如下表:
所以,函数f(x)的单调递增区间是(0,a+1),单调递减区间是(a,0)和(a+1,+∞).…(4分)
(II)证明:当-1<a<2(ln2-1)<0时,
由(I)知,f(x)的极小值为f(0),极大值为f(a+1).
因为f(0)=aln(-a)>0, ,
,
且f(x)在(a+1,+∞)上是减函数,
所以f(x)至多有一个零点.
又因为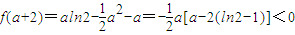 ,
,
所以函数f(x)只有一个零点x,且a+1<x<a+2.…(9分)
(III)解:因为 ,
,
所以任意x1,x2∈[0,x]且x2-x1=1,
由(II)可知x1∈[0,a+1],x2∈(a+1,x],且x2≥1.
因为函数f(x)在[0,a+1]上是增函数,在(a+1,+∞)上是减函数,
所以f(x1)≥f(0),f(x2)≤f(1),
∴f(x1)-f(x2)≥f(0)-f(1).
当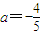 时,
时,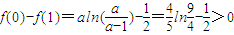 .
.
所以f(x1)-f(x2)≥f(0)-f(1)>0
所以|f(x2)-f(x1)|的最小值为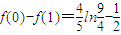 .
.
所以使得|f(x2)-f(x1)|≥m恒成立的m的最大值为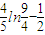 .…(14分)
.…(14分)
点评:本题考查函数的单调区间的求法,考查不等式的证明,考查满足条件的实数的最大值的求法,考查推理论证能力,考查等价转化思想,解题时要认真审题,注意导数性质的合理运用.
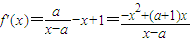 .由此能求出题函数f(x)的单调区间.
.由此能求出题函数f(x)的单调区间.(II)当-1<a<2(ln2-1)<0时,由(I)知,f(x)的极小值为f(0),极大值为f(a+1).由此能够证明函数f(x)只有一个零点x,且a+1<x<a+2.
(III)因为
 ,所以任意x1,x2∈[0,x]且x2-x1=1,由(II)可知x1∈[0,a+1],x2∈(a+1,x],且x2≥1.由此能推导出使得|f(x2)-f(x1)|≥m恒成立的m的最大值.
,所以任意x1,x2∈[0,x]且x2-x1=1,由(II)可知x1∈[0,a+1],x2∈(a+1,x],且x2≥1.由此能推导出使得|f(x2)-f(x1)|≥m恒成立的m的最大值.解答:(I)解:f(x)的定义域为(a,+∞).
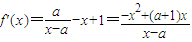 .
.令f'(x)=0⇒x=0或x=a+1.
当-1<a<0时,a+1>0,函数f(x)与f'(x)随x的变化情况如下表:
| x | (a,0) | (0,a+1) | a+1 | (a+1,+∞) | |
| f(x) | - | + | - | ||
| f'(x) | ↘ | 极小值 | ↗ | 极大值 | ↘ |
(II)证明:当-1<a<2(ln2-1)<0时,
由(I)知,f(x)的极小值为f(0),极大值为f(a+1).
因为f(0)=aln(-a)>0,
 ,
,且f(x)在(a+1,+∞)上是减函数,
所以f(x)至多有一个零点.
又因为
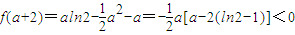 ,
,所以函数f(x)只有一个零点x,且a+1<x<a+2.…(9分)
(III)解:因为
 ,
,所以任意x1,x2∈[0,x]且x2-x1=1,
由(II)可知x1∈[0,a+1],x2∈(a+1,x],且x2≥1.
因为函数f(x)在[0,a+1]上是增函数,在(a+1,+∞)上是减函数,
所以f(x1)≥f(0),f(x2)≤f(1),
∴f(x1)-f(x2)≥f(0)-f(1).
当
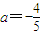 时,
时,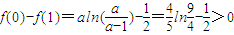 .
.所以f(x1)-f(x2)≥f(0)-f(1)>0
所以|f(x2)-f(x1)|的最小值为
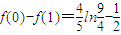 .
.所以使得|f(x2)-f(x1)|≥m恒成立的m的最大值为
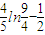 .…(14分)
.…(14分)点评:本题考查函数的单调区间的求法,考查不等式的证明,考查满足条件的实数的最大值的求法,考查推理论证能力,考查等价转化思想,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. .
. ,
, .
.