题目内容
有下列命题:
①已知 是平面内两个非零向量,则平面内任一向量
是平面内两个非零向量,则平面内任一向量 都可表示为
都可表示为 ,其中
,其中 ;
;
②对任意平面四边形ABCD,点E、F分别为AB、CD的中点,则 ;
;
③直线 的一个方向向量为
的一个方向向量为 ;
;
④已知 与
与 夹角为
夹角为 ,且
,且 ·
· =
= ,则|
,则| -
- |的最小值为
|的最小值为 ;
;
⑤ 是(
是( ·
· )·
)· =
= ·(
·( ·
· )的充分条件;
)的充分条件;
其中正确的是 (写出所有正确命题的编号).
【答案】
②④⑤.
【解析】
试题分析:①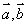 是平面内两个非零向量,若
是平面内两个非零向量,若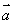 ∥
∥ ,不能用
,不能用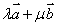 表示平面内任一向量,故①错;②对任意平面四边形
表示平面内任一向量,故①错;②对任意平面四边形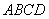 中,
中,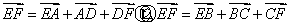 ,又点
,又点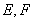 分别为
分别为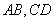 的中点,
的中点,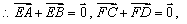 由①+②可得
由①+②可得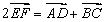 ,故②正确;③
,故②正确;③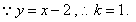 故直线
故直线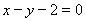 的一个方向向量为
的一个方向向量为 ,故③错;④
,故③错;④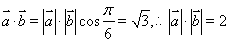 .又
.又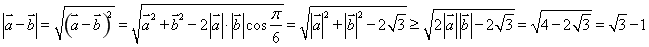
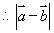 的最小值为
的最小值为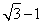 ,故④正确;⑤若
,故④正确;⑤若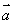 ∥
∥ ,即
,即
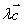 ,又
,又 和
和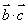 为常数,
为常数, 反之亦成立,故⑤成立.综上得正确的是②④⑤.
反之亦成立,故⑤成立.综上得正确的是②④⑤.
考点:1.平面向量共线的充要条件;2.平面向量基本定理;3.向量加法的平行四边形法则;4.向量的数量积运算.

练习册系列答案
相关题目
 ”是“|2y-x|≤2”的充分不必要条件.
”是“|2y-x|≤2”的充分不必要条件. =
=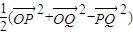 ;
;