题目内容
直线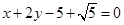 被圆
被圆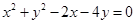 截得的弦长为 ( )
截得的弦长为 ( )
| A.1 | B.2 | C.3 | D.4 |
D
解析试题分析:将圆化为标准方程得: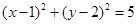 ,圆心坐标为(1,2),半径为
,圆心坐标为(1,2),半径为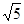 ,圆心到直线的距离
,圆心到直线的距离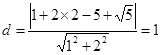 ,则直线被圆截得的弦长为
,则直线被圆截得的弦长为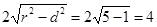 .
.
考点:此题考查了直线与圆相交的性质,涉及的知识有:垂径定理,勾股定理,点到直线的距离公式,以及圆的标准方程,熟练掌握垂径定理是解本题的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
圆 上的点到直线
上的点到直线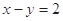 的距离最大值是( )
的距离最大值是( )
A. | B.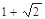 | C.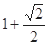 | D.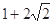 |
过点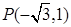 的直线
的直线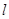 与圆
与圆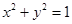 有公共点,则直线
有公共点,则直线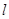 的倾斜角的取值范围是( )
的倾斜角的取值范围是( )
A.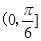 | B.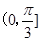 | C.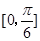 | D.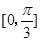 |
已知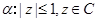 ,
,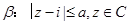 .若
.若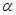 是
是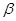 的充分非必要条件,则实数
的充分非必要条件,则实数 的取值范围是( )
的取值范围是( )
A.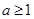 | B.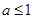 | C.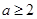 | D.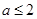 |
若直线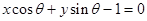 与圆
与圆 相切,且
相切,且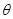 为锐角,则这条直线的斜率是( )
为锐角,则这条直线的斜率是( )
A.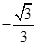 | B.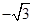 | C. | D.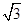 |
如果圆 上总存在两个点到原点的距离为
上总存在两个点到原点的距离为 则实数a的取值范围是
则实数a的取值范围是
A. | B.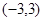 | C.[-1,1] | D. |
若圆C的半径为1,圆心在第一象限,且与直线4x-3y=0和x轴都相切,则该圆
的标准方程是 ( )
| A.(x-2)2+(y-1)2=1 |
| B.(x-2)2+(y+1)2=1 |
| C.(x+2)2+(y-1)2=1 |
| D.(x-3)2+(y-1)2=1 |
直线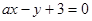 与圆
与圆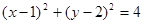 相交于
相交于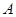 、
、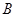 两点且
两点且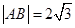 ,则a的值为( )
,则a的值为( )
| A.3 | B.2 | C.1 | D.0 |
 和圆:
和圆: 交于A、B两点,则AB的垂直平分线的方程是( ).
交于A、B两点,则AB的垂直平分线的方程是( ). B.
B. C.
C.  D.
D.