ĢāÄæÄŚČŻ
”¾ĢāÄæ”æÄ³ŃŠ¾æŠŌѧĻ°Š”×飬ĪŖĮĖ¶Ō°×ĢģĘ½¾łĘųĪĀÓėijÄĢ²čµźµÄijÖÖŅūĮĻĻśĮæÖ®¼äµÄ¹ŲĻµ½ųŠŠ·ÖĪöŃŠ¾æ£¬ĖūĆĒ·Ö±š¼ĒĀ¼ĮĖ2ŌĀ11ČÕÖĮ2ŌĀ16Čյİ×ĢģĘ½¾łĘųĪĀx£Ø”ę£©ÓėøĆÄĢ²čµźµÄÕāÖÖŅūĮĻĻśĮæy£Ø±£©£¬µĆµ½ČēĻĀŹż¾Ż£ŗ
ČÕĘŚ | 2ŌĀ11ČÕ | 2ŌĀ12ČÕ | 2ŌĀ13ČÕ | 2ŌĀ14ČÕ | 2ŌĀ15ČÕ | 2ŌĀ16ČÕ |
Ę½¾łĘųĪĀx£Ø”ę£© | 10 | 11 | 13 | 12 | 8 | 6 |
ŅūĮĻĻśĮæy£Ø±£© | 22 | 25 | 29 | 26 | 16 | 12 |
øĆŠ”×éµÄŃŠ¾æ·½°ø£ŗĻČ“ÓÕāĮł×鏿¾ŻÖŠŃ”Č”2×飬ÓĆŹ£ĻĀµÄ4×鏿¾ŻĒóĻߊŌ»Ų¹é·½³Ģ£¬ŌŁÓƱ»Ń”µÄ2×鏿¾Ż½ųŠŠ¼ģŃ飮
£Ø¢ń£©ĒóєȔµÄ2×鏿¾ŻĒ”ŗĆŹĒĻąĮŚĮ½ĢģµÄøÅĀŹ£»
£Ø¢ņ£©ČōєȔµÄŹĒ11ČÕŗĶ16ČÕµÄĮ½×鏿¾Ż£¬Ēėøł¾Ż12ČÕÖĮ15ČÕµÄŹż¾Ż£¬Ēó³öy¹ŲÓŚxµÄĻߊŌ»Ų¹é·½³Ģ![]() £½
£½![]() x£«
x£«![]() £¬²¢ÅŠ¶ĻøĆŠ”×éĖłµĆĻߊŌ»Ų¹é·½³ĢŹĒ·ńĄķĻė£®£ØČōÓÉĻߊŌ»Ų¹é·½³ĢµĆµ½µÄ¹Ą¼ĘŹż¾ŻÓėĖłŃ”µÄ¼ģŃ鏿¾ŻµÄĪó²ī¾ł²»³¬¹ż2±£¬ŌņČĻĪŖøĆ·½³ĢŹĒĄķĻėµÄ£©
£¬²¢ÅŠ¶ĻøĆŠ”×éĖłµĆĻߊŌ»Ų¹é·½³ĢŹĒ·ńĄķĻė£®£ØČōÓÉĻߊŌ»Ų¹é·½³ĢµĆµ½µÄ¹Ą¼ĘŹż¾ŻÓėĖłŃ”µÄ¼ģŃ鏿¾ŻµÄĪó²ī¾ł²»³¬¹ż2±£¬ŌņČĻĪŖøĆ·½³ĢŹĒĄķĻėµÄ£©
”¾“š°ø”æ£ØI£©![]() £»£ØII£©
£»£ØII£©![]() £¬¾¼ģŃ飬ĖłµĆ»Ų¹éÖ±Ļß·½³ĢŹĒĄķĻėµÄ£®
£¬¾¼ģŃ飬ĖłµĆ»Ų¹éÖ±Ļß·½³ĢŹĒĄķĻėµÄ£®
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗ£ØI£©“Ó![]() ĢģÖŠČĪŃ”
ĢģÖŠČĪŃ”![]() Ģģ£¬ĖłÓŠæÉÄܵĽį¹ūĪŖ£ŗ
Ģģ£¬ĖłÓŠæÉÄܵĽį¹ūĪŖ£ŗ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬¹²
£¬¹²![]() øö£¬ÉčŹĀ¼ž
øö£¬ÉčŹĀ¼ž![]() ”°Ń”Č”µÄ
”°Ń”Č”µÄ![]() ×鏿¾ŻĒ”ŗĆŹĒĻąĮŚĮ½Ģģ”±£¬Ōņ
×鏿¾ŻĒ”ŗĆŹĒĻąĮŚĮ½Ģģ”±£¬Ōņ![]() °üŗ¬
°üŗ¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() ¹²
¹²![]() øö»ł±¾ŹĀ¼ž£¬ĖłŅŌ
øö»ł±¾ŹĀ¼ž£¬ĖłŅŌ![]() £»£ØII£©
£»£ØII£©![]() £¬
£¬
![]() £¬Éč»Ų¹éÖ±Ļß·½³ĢĪŖ
£¬Éč»Ų¹éÖ±Ļß·½³ĢĪŖ![]() £¬
£¬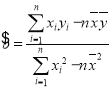 £¬øł¾Ż»Ų¹éÖ±Ļß·½³Ģ¹ż
£¬øł¾Ż»Ų¹éÖ±Ļß·½³Ģ¹ż![]() £¬æÉŅŌĒó³ö
£¬æÉŅŌĒó³ö![]() £¬Č»ŗóæÉŅŌ½«
£¬Č»ŗóæÉŅŌ½«![]() ČÕŗĶ
ČÕŗĶ![]() ČÕµÄŹż¾Ż“śČė¼ģŃ飬“Ó¶ųÅŠ¶ĻĖłµĆµÄ»Ų¹éÖ±Ļß·½³ĢŹĒ·ńĄķĻė£®
ČÕµÄŹż¾Ż“śČė¼ģŃ飬“Ó¶ųÅŠ¶ĻĖłµĆµÄ»Ų¹éÖ±Ļß·½³ĢŹĒ·ńĄķĻė£®
ŹŌĢā½āĪö£ŗ£ØI£©É蔰єȔµÄ2×鏿¾ŻĒ”ŗĆŹĒĻąĮŚ2ĢģŹż¾Ż”±ĪŖŹĀ¼žA£¬
”ßĖłÓŠ»ł±¾ŹĀ¼ž£Øm£¬n£©£ØĘäÖŠm£¬nĪŖ2ŌĀ·ŻµÄČÕĘŚŹż£©ÓŠ£ŗ
£Ø11,12£©£¬£Ø11,13£©£¬£Ø11,14£©£¬£Ø11,15£©£¬£Ø11,16£©£¬£Ø12,13£©£¬£Ø12,14£©£¬£Ø12,15£©£¬£Ø12,16£©£¬£Ø13,14£©£¬£Ø13,15£©£¬£Ø13,16£©£¬£Ø14,15£©£¬£Ø14,16£©£¬£Ø15,16£©¹²15øö£®
ŹĀ¼žA°üĄØµÄ»ł±¾ŹĀ¼žÓŠ£Ø11,12£©£¬£Ø12,13£©£¬£Ø13,14£©£¬£Ø14,15£©£¬£Ø15,16£©¹²5øö£®
”ą³é³öµÄ2×鏿¾ŻĒ”ŗĆŹĒĻąĮŚ2ĢģŹż¾ŻµÄøÅĀŹ![]() 4·Ö
4·Ö
£ØII£©”ß![]() £¬
£¬
![]() £®
£®
”ąÓɹ«Ź½£¬ĒóµĆ![]() £¬
£¬![]() £¬
£¬
”ą![]() ¹ŲÓŚ
¹ŲÓŚ![]() µÄĻߊŌ»Ų¹é·½³ĢĪŖ
µÄĻߊŌ»Ų¹é·½³ĢĪŖ![]() £¬ 8·Ö
£¬ 8·Ö
”ßµ±![]() Ź±£¬
Ź±£¬![]() £¬
£¬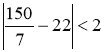 £¬
£¬
µ±![]() Ź±£¬
Ź±£¬![]() £¬
£¬ £¬
£¬
”ąøĆŠ”×éĖłµĆĻߊŌ»Ų¹é·½³ĢŹĒĄķĻėµÄ£® 12·Ö

 æŚĖćĢāæر±¾©ø¾Å®¶łĶƳö°ęÉēĻµĮŠ“š°ø
æŚĖćĢāæر±¾©ø¾Å®¶łĶƳö°ęÉēĻµĮŠ“š°ø

