题目内容
底面是矩形的四棱柱ABCD-A′B′C′D′中,AB=4,AD=3,AA′=5,∠BAD=90°,∠BAA′=∠DAA′=60°,则AC′=( )A.
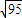
B.
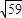
C.
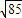
D.
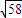
【答案】分析:连接AC,根据cos∠A'AB=cos∠A'AC•cos∠CAB求出∠A'AC,根据互补性可知∠C'CA的大小,最后根据余弦定理得求出AC′即可.
解答: 解:连接AC,∵AB=4,AD=3,∠BAD=90°
解:连接AC,∵AB=4,AD=3,∠BAD=90°
∴AC=5
根据cos∠A'AB=cos∠A'AC•cos∠CAB
即 =cos∠A'AC•
=cos∠A'AC•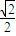
∴∠A'AC=45°则∠C'CA=135°
而AC=5,AA′=5,
根据余弦定理得AC′=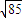
故选:C
点评:本题主要考查了体对角线的求解,以及余弦定理的应用,同时考查了空间想象能力,计算推理的能力,属于中档题.
解答:
 解:连接AC,∵AB=4,AD=3,∠BAD=90°
解:连接AC,∵AB=4,AD=3,∠BAD=90°∴AC=5
根据cos∠A'AB=cos∠A'AC•cos∠CAB
即
 =cos∠A'AC•
=cos∠A'AC•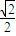
∴∠A'AC=45°则∠C'CA=135°
而AC=5,AA′=5,
根据余弦定理得AC′=
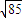
故选:C
点评:本题主要考查了体对角线的求解,以及余弦定理的应用,同时考查了空间想象能力,计算推理的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目