题目内容
【题目】在三棱锥D-ABC中,![]() ,且
,且![]() ,
,![]() ,M,N分别是棱BC,CD的中点,下面结论正确的是( )
,M,N分别是棱BC,CD的中点,下面结论正确的是( )
A.![]() B.
B.![]() 平面ABD
平面ABD
C.三棱锥A-CMN的体积的最大值为![]() D.AD与BC一定不垂直
D.AD与BC一定不垂直
【答案】ABD
【解析】
根据题意画出三棱锥D-ABC,取![]() 中点
中点![]() ,连接
,连接![]() :对于A,根据等腰三角形性质及线面垂直判定定理可证明
:对于A,根据等腰三角形性质及线面垂直判定定理可证明![]() 平面
平面![]() ,从而即可判断A;对于B,由中位线定理及线面平行判定定理即可证明;对于C,当平面
,从而即可判断A;对于B,由中位线定理及线面平行判定定理即可证明;对于C,当平面![]() 平面
平面![]() 时,三棱锥A-CMN的体积最大,由线段关系及三棱锥体积公式即可求解;对于D,假设
时,三棱锥A-CMN的体积最大,由线段关系及三棱锥体积公式即可求解;对于D,假设![]() ,通过线面垂直判定定理可得矛盾,从而说明假设不成立,即可说明原命题成立即可.
,通过线面垂直判定定理可得矛盾,从而说明假设不成立,即可说明原命题成立即可.
根据题意,画出三棱锥D-ABC如下图所示,取![]() 中点
中点![]() ,连接
,连接![]() :
:
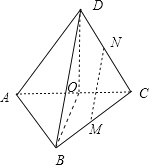
对于A,因为![]() ,且
,且![]() ,
,![]() ,
,
所以![]() 为等腰直角三角形,
为等腰直角三角形,
则![]() 且
且![]() ,
,
则![]() 平面
平面![]() ,
,
所以![]() ,即A正确;
,即A正确;
对于B,因为M,N分别是棱BC,CD的中点,
由中位线定理可得![]() ,而
,而![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,即B正确;
,即B正确;
对于C,当平面![]() 平面
平面![]() 时,三棱锥A-CMN的体积最大,
时,三棱锥A-CMN的体积最大,
则最大值为![]() ,即C错误;
,即C错误;
对于D,假设![]() ,由
,由![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() ,则
,则![]() ,
,
又因为![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() ,由
,由![]() 平面
平面![]() ,则
,则![]() ,
,
由题意可知![]() ,因而
,因而![]() 不能成立,因而假设错误,所以D正确;
不能成立,因而假设错误,所以D正确;
综上可知,正确的为ABD,
故选:ABD.

练习册系列答案
相关题目

