题目内容
已知函数f(x)＝Atan(ωx＋φ)
，y＝f(x)的部分图像如图，则f
＝________.
，y＝f(x)的部分图像如图，则f＝________.
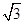
解析：由图像可知，此正切函数的半周期等于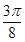
－
＝
＝
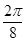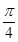，即周期为
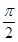，所以ω＝2.由题意可知，图像过定点
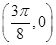，所以0＝Atan2×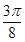＋φ，即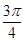
＋φ＝kπ(k∈Z)，所以φ＝kπ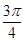－ (k∈Z)，又|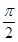φ|<，所以φ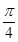＝.再由图像过定点(0,1)，可得A＝1.综上可知，f(x)＝tan
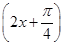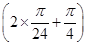.故有f＝tan
＝tan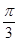
＝.
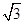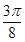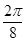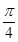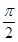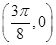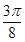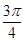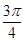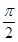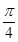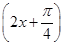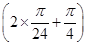－＝＝，即周期为，所以ω＝2.由题意可知，图像过定点，所以0＝Atan2×＋φ，即＋φ＝kπ(k∈Z)，所以φ＝kπ－ (k∈Z)，又|φ|<，所以φ＝.再由图像过定点(0,1)，可得A＝1.综上可知，f(x)＝tan.故有f＝tan＝tan＝.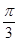
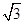练习册系列答案
相关题目
． 的部分图象如图所示，其中点
是图象的一个最高点.
的解析式；
且
，求
．
，图象关于点（
，0）对称”两个性质的函数是（ ）
)+f(x)=0,则ω的值为( )
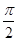，直线x＝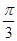
是其图像的一条对称轴，则下列各式中符合条件的解析式为( )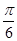
<φ<
.
的图像上各点向右平移
个单位，则得到新函数的解析式为( )
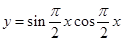的周期是 .