题目内容
设x，y∈R，Z=x+yi，Z满足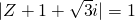
，则|Z|的最大值为
- A.1
- B.2
- C.3
- D.4
C
分析：由题意得，Z满足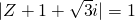，则满足条件的复数z在以A（-1，-
）为圆心，以1为半径的圆上，
所求的最大值为|OA|加上半径1．
解答：∵x，y∈R，Z=x+yi，Z满足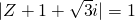，则满足条件的复数z在以A（-1，-）为圆心，
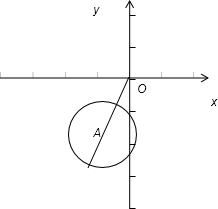
以1为半径的圆上，如图所示：
|Z|表示复平面内的点Z到原点的距离，其最大值为|OA|加上半径1，|OA|=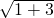
=2，
故|Z|的最大值为3，
故选 C．
点评：本题考查复数代数形式的混合运算，复数与复平面内对应点之间的关系，复数的模的定义，判断满足条件的复数z在
以A（-1，-）为圆心、以1为半径的圆上，是解题的关键．
分析：由题意得，Z满足
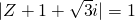，则满足条件的复数z在以A（-1，-）为圆心，以1为半径的圆上，所求的最大值为|OA|加上半径1．
解答：∵x，y∈R，Z=x+yi，Z满足
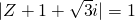，则满足条件的复数z在以A（-1，-）为圆心，以1为半径的圆上，如图所示：
|Z|表示复平面内的点Z到原点的距离，其最大值为|OA|加上半径1，|OA|=
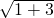=2，故|Z|的最大值为3，
故选 C．
点评：本题考查复数代数形式的混合运算，复数与复平面内对应点之间的关系，复数的模的定义，判断满足条件的复数z在
以A（-1，-
）为圆心、以1为半径的圆上，是解题的关键． 
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
设x，y∈R，Z=x+yi，Z满足|Z+1+
i|=1，则|Z|的最大值为（ ）
| 3 |
| A、1 | B、2 | C、3 | D、4 |
设命题p：?α0，β0∈R，cos（α0-β0）=cosα0+cosβ0；命题q：?x，y∈R，且x≠
+kπ，y≠
+kπ，k∈Z，若x＞y，则tanx＞tany，则下列命题中真命题是（ ）
| π |
| 2 |
| π |
| 2 |
| A、p∧q |
| B、p∧（￢q） |
| C、（￢p）∧q |
| D、（￢p）∧（￢q） |