题目内容
设x、y∈R,满足x≤2,y≤3,且x+y=3,则z=4x3+y3的最大值为
[ ]
A.
24
B.
27
C.
33
D.
45
答案:C
解析:
解析:
|
由y=3-x置换z=4x3+y3里面的y,建立z的目标函数,应用导函数求最值,但要注意x的取值范围. 由 ∵z=4x3+y3=4x3+(3-x)3=3x3+9x2-27x+27, ∴ ∵z在(0,1)上单调递减,在(1,2)单调递增,z(0)=27,z(2)=33. 故当x=2时,zmax=33. |

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
设x,y∈R,Z=x+yi,Z满足|Z+1+
i|=1,则|Z|的最大值为( )
| 3 |
| A、1 | B、2 | C、3 | D、4 |
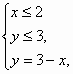 得0≤x≤2.
得0≤x≤2.