题目内容
17．
如图所示的几何体中，四边形ABCD为矩形，AD⊥平面AEB，AE=EB=BC=2，F为CE上的点，且BF⊥平面ACE．（1）求证：AE∥平面BFD；
（2）求三棱锥C-BGF的体积．
分析 （1）由题意可得G为AC中点，再由已知可得F是EC中点，连接FG，由三角形中位线性质可得FG∥AE，再由线面平行的判定得答案；
（2）把三棱锥C-BGF的体积转化为G-BFC的体积，然后通过解三角形求得三棱锥G-BFC的底面积和高，则三棱锥的体积可求．
解答 （1）证明：如图，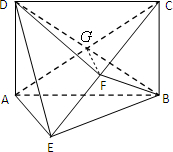
由题意可得G是AC的中点，连接FG，
∵BF⊥平面ACE，则CE⊥BF，而BC=BE，
∴F是EC中点，
在△AEC中，FG∥AE，∴AE∥平面BFD；
（2）解：∵AE∥平面BFD，∴AE∥FG，
由题可得AE⊥平面BCE，∴FG⊥平面BCE．
∵G是AC的中点，F是CE中点，∴AE∥FG且FG=$\frac{1}{2}AE=1$，
∵BF⊥平面ACE，∴BF⊥CE，∴Rt△BCE中，BF=$\frac{1}{2}CE=CF=\sqrt{2}$，
∴${S}_{△CFB}=\frac{1}{2}×\sqrt{2}×\sqrt{2}=1$，
∴${V}_{C-BGF}={V}_{G-BCF}=\frac{1}{3}{S}_{△CFB}•FG$=$\frac{1}{3}$．
点评 本小题主要考查空间线面关系、几何体的体积等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力，是中档题．
练习册系列答案
相关题目
9．若复数Z的实部为1，且|Z|=2，则复数Z的虚部是（ ）
| A． | -$\sqrt{3}$ | B． | ±$\sqrt{3}$ | C． | ±$\sqrt{3}$i | D． | $\sqrt{3}$i |
如图，四棱锥P-ABCD的底面ABCD是正方形，棱PD⊥底面ABCD，PD=2，∠PCD=45°，E是PC的中点．
如图，已知四边形ABCD，EADM，MDCF都是边长为2的正方形，点P，Q分别是ED，AC的中点．
6．设函数$f（x）=3sin（2x+\frac{π}{4}）+1$，将y=f（x）的图象向右平移φ（φ＞0）个单位，使得到的图象关于y对称，则φ的最小值为（ ）
| A． | $\frac{π}{8}$ | B． | $\frac{π}{4}$ | C． | $\frac{3π}{8}$ | D． | $\frac{3π}{4}$ |