题目内容
【题目】已知椭圆![]() :
:![]()
![]() 的长轴长是短轴长的
的长轴长是短轴长的![]() 倍,点
倍,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若过椭圆的左焦点的直线![]() 与椭圆
与椭圆![]() 相交所得弦长为
相交所得弦长为![]() ,求直线
,求直线![]() 的斜率;
的斜率;
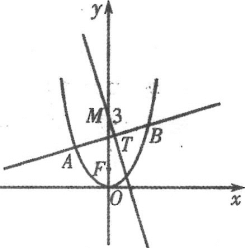
(3)过点![]() 的任意直线与椭圆
的任意直线与椭圆![]() 交于
交于![]() 、
、![]() 两点,设点
两点,设点![]() 、
、![]() 到直线
到直线![]() :
:![]() 的距离分别为
的距离分别为![]() .若
.若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用长轴长是短轴长的![]() 倍,点
倍,点![]() 在椭圆
在椭圆![]() 上,建立方程组求解;
上,建立方程组求解;
(2)联立方程,结合弦长可求直线![]() 的斜率;
的斜率;
(3)把![]() 转化为
转化为![]() 坐标间的关系,结合韦达定理可求.
坐标间的关系,结合韦达定理可求.
(1)由题意![]() ,则方程化为
,则方程化为![]() ,
,
因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,解得
,解得![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,
,
联立 得
得![]() ,
,
设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,
则![]() ,
,![]() ,
,

![]() ,
,
解得![]() ,故直线
,故直线![]() 的斜率为
的斜率为![]() .
.
(3)当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 恒成立;
恒成立;
当直线![]() 的斜率为0时,由
的斜率为0时,由![]() 得
得![]() ,即
,即![]() ;
;
当直线![]() 的斜率存在且不为0时,设
的斜率存在且不为0时,设![]() ,
,![]() .
.
联立 得
得![]() ,
,
设![]() ,不妨设
,不妨设![]() ,
,
则![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
整理可得![]() ,
,
![]()
解得![]() .
.
综上可得![]() .
.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案【题目】某共享单车经营企业欲向甲市投放单车,为制定适宜的经营策略,该企业首先在已投放单车的乙市进行单车使用情况调查.调查过程分随机问卷、整理分析及开座谈会三个阶段.在随机问卷阶段,A,B两个调查小组分赴全市不同区域发放问卷并及时收回;在整理分析阶段,两个调查小组从所获取的有效问卷中,针对15至45岁的人群,按比例随机抽取了300份,进行了数据统计,具体情况如下表:
组别 年龄 | A组统计结果 | B组统计结果 | ||
经常使用单车 | 偶尔使用单车 | 经常使用单车 | 偶尔使用单车 | |
| 27人 | 13人 | 40人 | 20人 |
| 23人 | 17人 | 35人 | 25人 |
| 20人 | 20人 | 35人 | 25人 |
(1)先用分层抽样的方法从上述300人中按“年龄是否达到35岁”抽出一个容量为60人的样本,再用分层抽样的方法将“年龄达到35岁”的被抽个体数分配到“经常使用单车”和“偶尔使用单车”中去.求这60人中“年龄达到35岁且偶尔使用单车”的人数;
(2)从统计数据可直观得出“是否经常使用共享单车与年龄(记作![]() 岁)有关”的结论.在用独立性检验的方法说明该结论成立时,为使犯错误的概率尽可能小,年龄
岁)有关”的结论.在用独立性检验的方法说明该结论成立时,为使犯错误的概率尽可能小,年龄![]() 应取25还是35?请通过比较
应取25还是35?请通过比较![]() 的观测值的大小加以说明.
的观测值的大小加以说明.
参考公式:![]() ,其中
,其中![]() .
.