题目内容
设集合M={1,2,3,4,5,6},S1,S2,…,SK都是M的含两个元素的子集,从中任选两个Si,Sj,Si={ai,bi},Sj={aj,bj},(i≠j),i,j∈{1,2,3,…,k},则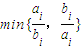 ≠
≠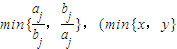 表示两个数x,y中的较小者)的概率等于 .
表示两个数x,y中的较小者)的概率等于 .
【答案】分析:根据题意,对于M,含2个元素的子集有15个,所以从中任选两个Si,Sj,的所有选法有:C152=105个,找出不符合题意的共有三组,计算出不符合题意的选法,即可得到符合题意的选法,进而求出事件发生的概率.
解答:解:根据题意,对于M,含2个元素的子集有15个,
所以从中任选两个Si,Sj,的所有选法有:C152=105个,
由题意可得不符合题意的共有三组,分别为:{1,2}、{2,4}、{3,6};{1,3}、{2,6};{2,3}、{4,6},
所以不符合题意的选法共有:C32+1+1=5个,
所以符合题意的选法共有100个,
所以其发生的概率为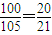 .
.
故答案为: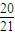 .
.
点评:本题考查学生对集合及其子集、元素的把握、运用,以及等可能事件发生的概率,解决此类问题的关键是正确理解新定义.
解答:解:根据题意,对于M,含2个元素的子集有15个,
所以从中任选两个Si,Sj,的所有选法有:C152=105个,
由题意可得不符合题意的共有三组,分别为:{1,2}、{2,4}、{3,6};{1,3}、{2,6};{2,3}、{4,6},
所以不符合题意的选法共有:C32+1+1=5个,
所以符合题意的选法共有100个,
所以其发生的概率为
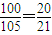 .
.故答案为:
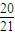 .
.点评:本题考查学生对集合及其子集、元素的把握、运用,以及等可能事件发生的概率,解决此类问题的关键是正确理解新定义.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
设集合M={1,2},N={a2},则a=1是N?M的( )条件.
| A、充分不必要 | B、必要不充分 | C、充要 | D、既不充分也不必要 |
设集合M={1,2,3},N={1},则下列关系正确的是( )
| A、N∈M | B、N∉M | C、N=M | D、N?M |