题目内容
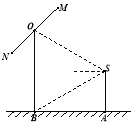
【题目】如图,△ABC为正三角形,且BC=CD=2,CD⊥BC,将△ABC沿BC翻折.
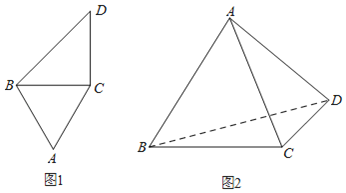
(1)当AD=2时,求证:平面ABD⊥平面BCD;
(2)若点A的射影在△BCD内,且直线AB与平面ACD所成角为60°,求AD的长.
【答案】(1)见解析(2)![]() .
.
【解析】
(1)根据长度关系得到AE⊥平面BCD,得到证明.
(2)取BC中点O,BD中点E,连接AO,OE,得HQ⊥平面ACD,计算HQ![]() ,AH
,AH![]() ,计算得到答案.
,计算得到答案.
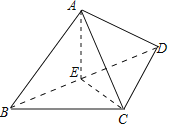
(1)若AD=2,又AB=AC=2,则A在底面BCD内的射影为△BCD的外心,
∵△BCD为直角三角形,且∠BCD=90°,
∴A在底面BCD内的射影E落在BD的中点上,
∴AE⊥平面BCD,而AE平面ABD,
∴平面ABD⊥平面BCD;
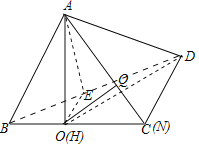
(2)取BC中点O,BD中点E,连接AO,OE,
可得BC⊥平面AOE,过A作AH⊥OE于H,过H作HN∥BC交CD于N,
连接AN,作HQ⊥AN于Q,得HQ⊥平面ACD,
点B到平面ACD的距离为2HQ,则sin60![]() ,得HQ
,得HQ![]() ,
,
设AH=x,有![]() ,解得x
,解得x![]() ,即AH
,即AH![]() ,
,
又AO![]() ,∴H与O重合,
,∴H与O重合,
则AD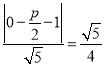 .
.

练习册系列答案
相关题目