题目内容
若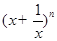 展开式中第四项与第六项的系数相等,则展开式中的常数项的值等于_________.
展开式中第四项与第六项的系数相等,则展开式中的常数项的值等于_________.
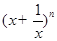 展开式中第四项与第六项的系数相等,则展开式中的常数项的值等于_________.
展开式中第四项与第六项的系数相等,则展开式中的常数项的值等于_________.70
试题分析:利用二项展开式的通项公式求出展开式的通项,求出第四项与第六项的系数,列出方程,求出n,令通项中的x为0,求出展开式的常数项. 解:展开式的通项为Tr+1=Cnrxn-2r,当r=3得第四项的系数为Cn3,当r=5得第六项的系数为Cn5,据题意知Cn3=Cn5,所以n=8,所以通项为Tr+1=C8rx8-2r,令8-2r=0得r=4,故展开式的常数项为C84=70,故答案为70.
点评:本题考查利用二项展开式的通项公式解决二项展开式的特定项问题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
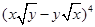 的展开式中,
的展开式中,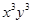 的系数是 。
的系数是 。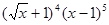 的展开式中,
的展开式中,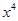 的系数为( )
的系数为( )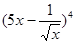 展开式中x的系数为 ( )
展开式中x的系数为 ( )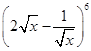 的展开式中不含
的展开式中不含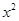 项的系数和是______
项的系数和是______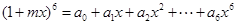 且
且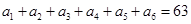 ,则实数m的值为 .
,则实数m的值为 .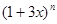 的各项系数和为
的各项系数和为 ,则
,则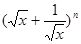 的常数项为 .
的常数项为 .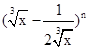 的展开式中,前三项系数的绝对值成等差数列
的展开式中,前三项系数的绝对值成等差数列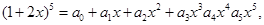 则a3= 。
则a3= 。