题目内容
14.已知a=cos1,b=cos2,c=sin2,则a、b、c的大小关系为( )| A. | a>b>c | B. | c>a>b | C. | a>c>b | D. | b>a>c |
分析 易得b为最小值,再和特殊角比较可得a和c的大小,可得答案.
解答 解:由题意可得b=cos2<0,a=cos1>0,c=sin2>0,
又a=cos1<cos$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$,c=sin2>sin$\frac{3π}{4}$=$\frac{\sqrt{2}}{2}$
∴c>a>b
故选:B
点评 本题考查三角函数值比较大小,属基础题.

练习册系列答案
相关题目
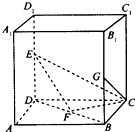 如图,棱长为1的正方体ABCD-A1B1C1D1,E,F,G分别是DD1,BD,BB1的中点.
如图,棱长为1的正方体ABCD-A1B1C1D1,E,F,G分别是DD1,BD,BB1的中点.