题目内容
20.设函数f(x)=|x+2|+a|x-3|(Ⅰ)当a=1时,求函数y=f(x)的最小值,并指出取得最小值时x的值;
(Ⅱ)若a≥1,讨论关于x的方程f(x)=a的解的个数.
分析 (Ⅰ)运用绝对值不等式的性质,即可得到最小值和相应x的范围;
(Ⅱ)$a=\frac{{|{x+2}|}}{{1-|{x-3}|}}$,设g(x)=$\frac{{|{x+2}|}}{{1-|{x-3}|}}$,运用分段函数的形式求出g(x),并求得各段的值域,对a讨论,即可得到解的个数.
解答 解:(Ⅰ)∵|x+2|+|x-3|≥|(x-2)-(x-3)|=5,
∴f(x)min=5,
当且仅当(x+2)(x-3)≤0,即有-2≤x≤3时f(x)取最小值;
(Ⅱ)$a=\frac{{|{x+2}|}}{{1-|{x-3}|}}$,设g(x)=$\frac{{|{x+2}|}}{{1-|{x-3}|}}$,
则g(x)=$\left\{\begin{array}{l}-\frac{x+2}{x-2},x≤-2\\ \frac{x+2}{x-2},-2<x≤3\\ \frac{x+2}{4-x},x>3\end{array}\right.$,可知,
当x≤-2时,g(x)=-1-$\frac{4}{x-2}$递增,有g(x)≤0;
当-2<x≤3时,g(x)=1+$\frac{4}{x-2}$,有g(x)≤0或g(x)≥5;
当x>3时,g(x)=-1-$\frac{6}{x-4}$,有g(x)>5或g(x)<-1.
故当a>5时,原方程有2个解;
当a=5时,原方程有1个解;
当1≤a<5时,原方程有0个解.
点评 本题考查函数的最值的求法和绝对值不等式的性质的运用,考查函数方程的转化思想的运用,运用分类讨论的思想方法是解题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
5.若a<b,d<c,且(c-a)(c-b)<0,(d-a)(d-b)>0,则a,b,c,d大小关系是( )
| A. | d<a<c<b | B. | d<c<a<b | C. | a<d<b<c | D. | a<d<c<b |
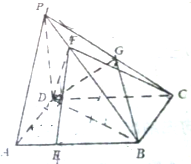 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC的中点,E,F分别为AB,PB上一点,AB=4$\sqrt{2}$,AE=$\sqrt{2}$,PB=4PF.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC的中点,E,F分别为AB,PB上一点,AB=4$\sqrt{2}$,AE=$\sqrt{2}$,PB=4PF.