题目内容
(2011•花都区模拟)已知函数f(x)=x2+alnx.
(1)当a=-2时,求函数f(x)的单调区间和极值;
(2)若g(x)=f(x)+
在[1,+∞)上是单调函数,求实数a的取值范围.
(1)当a=-2时,求函数f(x)的单调区间和极值;
(2)若g(x)=f(x)+
| 2 | x |
分析:(1)求出函数f(x)的导数,得到导数在x=1时为零.然后列表讨论函数在区间(0,1)和(1,+∞)上讨论函数的单调性,即可得到函数f(x)的单调区间和极值;
(2)g(x)=f(x)+
在[1,+∞)上是单调函数,说明g(x)的导数g'(x)在区间[1,+∞)恒大于等于0,或g'(x)在区间[1,+∞)恒小于等于0.然后分两种情况加以讨论,最后综合可得实数a的取值范围.
(2)g(x)=f(x)+
| 2 |
| x |
解答:解:(1)易知,函数f(x)的定义域为(0,+∞).…(1分)
当a=-2时,f′(x)=2x-
=
.…(2分)
当x变化时,f'(x)和f(x)的值的变化情况如下表:…(4分)
由上表可知,函数f(x)的单调递减区间是(0,1),单调递增区间是(1,+∞),极小值是f(1)=1.…(8分)
(2)由g(x)=x2+alnx+
,得g′(x)=2x+
-
.…(9分)
又函数g(x)=x2+alnx+
为[1,+∞)上单调函数,
①若函数g(x)为[1,+∞)上的单调增函数,
则g'(x)≥0在[1,+∞)上恒成立,
即不等式2x-
+
≥0在[1,+∞)上恒成立.
也即a≥
-2x2在[1,+∞)上恒成立,
而φ(x)=
-2x2在[1,+∞)上的最大值为φ(1)=0,所以a≥0.…(12分)
②若函数g(x)为[1,+∞)上的单调减函数,
根据①,在[1,+∞)上φ(x)max=φ(1)=0,φ(x)没有最小值.…(13分)
所以g'(x)≤0在[1,+∞)上是不可能恒成立的.…(15分)
综上,a的取值范围为[0,+∞).…(16分)
当a=-2时,f′(x)=2x-
| 2 |
| x |
| 2(x+1)(x-1) |
| x |
当x变化时,f'(x)和f(x)的值的变化情况如下表:…(4分)
| x | (0,1) | 1 | (1,+∞) |
| f'(x) | - | 0 | + |
| f(x) | 递减 | 极小值 | 递增 |
(2)由g(x)=x2+alnx+
| 2 |
| x |
| a |
| x |
| 2 |
| x2 |
又函数g(x)=x2+alnx+
| 2 |
| x |
①若函数g(x)为[1,+∞)上的单调增函数,
则g'(x)≥0在[1,+∞)上恒成立,
即不等式2x-
| 2 |
| x2 |
| a |
| x |
也即a≥
| 2 |
| x |
而φ(x)=
| 2 |
| x |
②若函数g(x)为[1,+∞)上的单调减函数,
根据①,在[1,+∞)上φ(x)max=φ(1)=0,φ(x)没有最小值.…(13分)
所以g'(x)≤0在[1,+∞)上是不可能恒成立的.…(15分)
综上,a的取值范围为[0,+∞).…(16分)
点评:本题是一道导数的应用题,着重考查利用导数研究函数的单调性与极值,函数恒成立等知识点,属于中档题.

练习册系列答案
相关题目
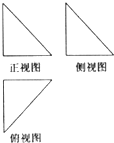 (2011•花都区模拟)如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为2,那么 这个几何体的体积为( )
(2011•花都区模拟)如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为2,那么 这个几何体的体积为( )