题目内容
15.解不等式:4cos2($\frac{π}{4}$-$\frac{1}{2}$x)>1.分析 由二倍角的余弦公式化简不等式后根据正弦函数的图象和性质即可求解.
解答 解:∵4cos2($\frac{π}{4}$-$\frac{1}{2}$x)=4×$\frac{1+cos[2×(\frac{π}{4}-\frac{1}{2}x)]}{2}$=2sinx+2>1
∴sinx>-$\frac{1}{2}$,
∴可解得:x∈(2kπ,2k$π+\frac{7π}{6}$)∪(2kπ$+\frac{11π}{6}$,2kπ+2π),k∈Z
点评 本题主要考查了二倍角的余弦公式,正弦函数的图象和性质的应用,属于基本知识的考查.

练习册系列答案
相关题目
20.将函数y=sin(2x+θ)的图象向右平移$\frac{π}{6}$个单位,得到的图象关于x=$\frac{π}{4}$对称,则θ的一个可能的值为( )
| A. | -$\frac{2}{3}π$ | B. | $\frac{2}{3}π$ | C. | -$\frac{5}{6}π$ | D. | $\frac{5}{6}π$ |
 与纵轴及直线
与纵轴及直线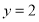 所围成的封闭图形为区域
所围成的封闭图形为区域 ,不等式组
,不等式组 所确定的区域为
所确定的区域为 ,在区域
,在区域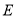 内随机取一点,该点恰好在区域
内随机取一点,该点恰好在区域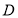 的概率为( )
的概率为( )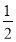 B.
B. C.
C. D. 以上答案均不正确
D. 以上答案均不正确 的内角
的内角 所对的边分别为
所对的边分别为 ,若
,若 ,
, ,则角
,则角 的度数为( )
的度数为( ) B.
B. C.
C. D.
D.
 与直线
与直线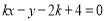 有两个相异的交点时,实数k的取值范围是( )
有两个相异的交点时,实数k的取值范围是( ) B.
B.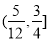 C.
C. D.
D.