��Ŀ����
��ԲG��| x2 |
| a2 |
| y2 |
| b2 |
| F1M |
| F2M |
��1���������ʵ�ȡֵ��Χ��
��2����������eȡ����Сֵʱ����N��0��3������Բ�ϵĵ����Զ����Ϊ5
| 2 |
�����ʱ��ԲG�ķ��̣�
����б��Ϊk��k��0����ֱ��L����ԲG�ཻ�ڲ�ͬ������A��B��QΪAB���е㣬��A��B�����ܷ���ڹ���P(0��-
| ||
| 3 |
���������⿼���֪ʶ����ƽ�����������������㣬��Բ�ı����̣���Բ�����ʼ�ֱ������Բ�Ĺ�ϵ��֪ʶ�㣬
��1��������M��x��y������������
��
�����꣬��
•
=0�����������ֱ�ij�Ҫ���������Ǽ��ɵõ�x��y�Ĺ�ϵʽ������M������Բ�ϣ�������Բ���̼��ɵõ������ʵ�ȡֵ��Χ��
��2�����ɣ�1���Ľ��ۣ������õ�������eȡ����Сֵʱ����Բ���̣������������ٵ�N��0��3������Բ�ϵĵ����Զ����Ϊ5
�������õ����ڲ����ķ��̣��ⷽ�̼��ɵõ���Բ�ķ��̣������δֱ֪�ߵķ��̣�Ȼ������ֱ�߷�������Բ���̣��õ�һ������x��һԪ���η��̣�Ȼ��ʹ�á�������ķ��������Τ�ﶨ����A��B�����ܷ���ڹ���P(0��-
)��Q��ֱ�߶Գƹ��첻��ʽ�飬�ⲻ��ʽ�鼴�ɵõ�k��ȡֵ��Χ��
��1��������M��x��y������������
| F1M |
| F2M |
| F1M |
| F2M |
��2�����ɣ�1���Ľ��ۣ������õ�������eȡ����Сֵʱ����Բ���̣������������ٵ�N��0��3������Բ�ϵĵ����Զ����Ϊ5
| 2 |
| ||
| 3 |
����⣺��1����M��x��y������
=(x+c��y)��
=(x-c��y)
��
•
=0?x2+y2=c2?y2=c2-x2��1�֣�
��M����Բ�ϣ���y2=b2-
x2��2�֣�
��c2-x2=b2-
x2?x2=a2-
����3�֣�
��0��x2��a2��0��2-
��1?
��e��1����4�֣�
��0��e��1����
��e��1��5�֣�
��2���ٵ�e=
ʱ����ԲΪ
+
=1
��H��x��y������Բ��һ�㣬
��|HN|2=x2+��y-3��2=��2b2-2y2��+��y-3��2=-��y+3��2+2b2+18����-b��y��b��
��6�֣�
��0��b��3����-3��-b��0����y=-bʱ��|HN|max2=b2+6b+9�����������b2+6b+9=50
��b=-3��5
����0��b��3ì�ܣ���7�֣�
��b��3��-b��-3����y=-3ʱ��|HN|max2=2b2+18������2b2+18=50��b2=16����������
����Բ�����ǣ�
+
=1��8�֣�
�ڣ���l��y=kx+m��
?(1+2k2)x2+4kmx+2m2-32=0
������0?m2��32k2+16��9�֣�
��A��B������ڹ���P(0��-
)��Q��ֱ�߶Գ�
��kPQ=-
����A��x1��y1����B��x2��y2������xQ=-
��yQ=
��10�֣�
��
=-
?m=
��11�֣�
��(
)2��32k2+16?0��k2��
��10�֣�
��k��0����-
��k��0��0��k��
��11�֣�
�������k��ȡֵ��Χ��-
��k��0��0��k��
��12�֣�
| F1M |
| F2M |
��
| F1M |
| F2M |
��M����Բ�ϣ���y2=b2-
| b2 |
| a2 |
��c2-x2=b2-
| b2 |
| a2 |
| a2b2 |
| c2 |
��0��x2��a2��0��2-
| 1 |
| e2 |
| ||
| 2 |
��0��e��1����
| ||
| 2 |
��2���ٵ�e=
| ||
| 2 |
| x2 |
| 2b2 |
| y2 |
| b2 |
��H��x��y������Բ��һ�㣬
��|HN|2=x2+��y-3��2=��2b2-2y2��+��y-3��2=-��y+3��2+2b2+18����-b��y��b��
��6�֣�
��0��b��3����-3��-b��0����y=-bʱ��|HN|max2=b2+6b+9�����������b2+6b+9=50
��b=-3��5
| 2 |
��b��3��-b��-3����y=-3ʱ��|HN|max2=2b2+18������2b2+18=50��b2=16����������
����Բ�����ǣ�
| x2 |
| 32 |
| y2 |
| 16 |
�ڣ���l��y=kx+m��
|
������0?m2��32k2+16��9�֣�
��A��B������ڹ���P(0��-
| ||
| 3 |
��kPQ=-
| 1 |
| k |
| 2km |
| 1+2k2 |
| m |
| 1+2k2 |
��
yQ+
| ||||
| xQ |
| 1 |
| k |
| 1+2k2 | ||
|
��(
| 1+2k2 | ||
|
| 47 |
| 2 |
��k��0����-
| ||
| 2 |
| ||
| 2 |
�������k��ȡֵ��Χ��-
| ||
| 2 |
| ||
| 2 |
�������ڴ���ֱ����Բ���ߵĹ�ϵ������ʱ�����ǵ�ʹ�õķ�����˼·һ���У����������̣����������Τ�ﶨ�������ҳ���ʽ�ȣ�

��ϰ��ϵ�д�
 ������ѧ��ʱ��ҵϵ�д�
������ѧ��ʱ��ҵϵ�д� ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д� ��������ϵ�д�
��������ϵ�д�
�����Ŀ
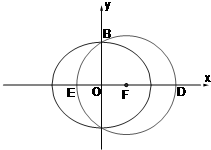 ��ͼ����֪F��c��0������Բ
��ͼ����֪F��c��0������Բ