题目内容
(2011•顺义区一模)已知椭圆G:
+
=1(a>b>0)的离心率e=
,且经过点P(1,
).
(Ⅰ)求椭圆G的方程;
(Ⅱ)设直线l:y=
x+m与椭圆G交于A、B两点,线段AB的垂直平分线交x轴于点T,当m变化时,求△TAB面积的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
| 2 |
(Ⅰ)求椭圆G的方程;
(Ⅱ)设直线l:y=
| 1 |
| 2 |
分析:(Ⅰ)根据椭圆的离心率e=
,且经过点P(1,
),结论方程组,即可求得椭圆G的方程;
(Ⅱ)直线l:y=
x+m与椭圆方程联立,利用韦达定理,进而可表示出三角形的面积,根据椭圆与直线有两个不同的交点,确定m的范围,即可求得△TAB面积的最大值.
| 1 |
| 2 |
| 3 |
| 2 |
(Ⅱ)直线l:y=
| 1 |
| 2 |
解答:解:(Ⅰ)由已知
,解得
----(2分)
∴椭圆G的方程为:
+
=1.----(4分)
(Ⅱ)
消去y得:x2+mx+m2-3=0,----(5分)
∵椭圆与直线有两个不同的交点,∴△>0,即m2<4,----(6分)
设A(x1,y1),B(x2,y2),AB的中点M(x0,y0)
∴x1+x2=-m,x1x2=m2-3,
∴|AB|=
=
,
x0=
=-
,y0=
x0+m=
m,∴M(-
,
m)----(8分)
设T(t,0),∵MT⊥AB,∴KMTKAB=-1,解得t=-
,----(10分)
∴T(-
,0),MT=
|m|,
∴S△TAB=
|AB|•|MT|=
,
∵0<m2<4----(12分)
∴当m2=2即m=±
时,△TAB面积最大为
----(14分)
|
|
∴椭圆G的方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)
|
∵椭圆与直线有两个不同的交点,∴△>0,即m2<4,----(6分)
设A(x1,y1),B(x2,y2),AB的中点M(x0,y0)
∴x1+x2=-m,x1x2=m2-3,
∴|AB|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
| ||
| 2 |
| 12-3m2 |
x0=
| x1+x2 |
| 2 |
| m |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| m |
| 2 |
| 3 |
| 4 |
设T(t,0),∵MT⊥AB,∴KMTKAB=-1,解得t=-
| m |
| 8 |
∴T(-
| m |
| 8 |
3
| ||
| 8 |
∴S△TAB=
| 1 |
| 2 |
| 15 |
| 32 |
| -3(m2-2)2+12 |
∵0<m2<4----(12分)
∴当m2=2即m=±
| 2 |
15
| ||
| 16 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查三角形面积的计算,正确表示三角形的面积是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
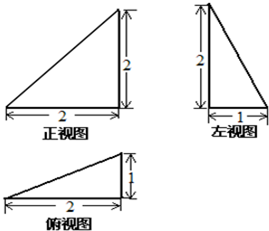 (2011•顺义区一模)一个几何体的三视图如图所示,则其表面积等于( )
(2011•顺义区一模)一个几何体的三视图如图所示,则其表面积等于( )