题目内容
(2013•海淀区一模)已知圆M:(x-
)2+y2=
,若椭圆C:
+
=1(a>b>0)的右顶点为圆M的圆心,离心率为
.
(I)求椭圆C的方程;
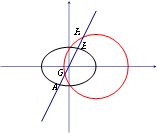
(II)已知直线l:y=kx,若直线l与椭圆C分别交于A,B两点,与圆M分别交于G,H两点(其中点G在线段AB上),且|AG|=|BH|,求k的值.
| 2 |
| 7 |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(I)求椭圆C的方程;
(II)已知直线l:y=kx,若直线l与椭圆C分别交于A,B两点,与圆M分别交于G,H两点(其中点G在线段AB上),且|AG|=|BH|,求k的值.
分析:(I)由圆心M(
,0)得到a=
.利用椭圆的离心率e=
及b2=a2-c2即可得出椭圆的标准方程;
(II)把直线l的方程与椭圆的方程联立,消去y得到关于x的一元二次方程,利用根与系数的关系及弦长公式即可得到|AB|,利用垂径定理及半径、弦长的一半、弦心距三者之间的关系(
)2=R2-d2即可得到|GH|,进而得出k.
| 2 |
| 2 |
| c |
| a |
(II)把直线l的方程与椭圆的方程联立,消去y得到关于x的一元二次方程,利用根与系数的关系及弦长公式即可得到|AB|,利用垂径定理及半径、弦长的一半、弦心距三者之间的关系(
| |GH| |
| 2 |
解答:解:(I)设椭圆的焦距为2c,由圆心M(
,0)得到a=
.
∵e=
=
,∴c=1.
∴b2=a2-c2=1.
所以椭圆C:
+y2=1.
(II)设A(x1,y1),B(x2,y2).
由直线l与椭圆C交于两点A,B,则
消去y得到(1+2k2)x2-2=0,则x1+x2=0,x1x2=-
.
∴|AB|=
=
.
点M(
,0)到直线l的距离d=
.
则|GH|=2
.
显然,若点H也在线段AB上,则由对称性可知,直线y=kx就是y轴,矛盾.
∵|AG|=|BH|,∴|AB|=|GH|.
∴
=4(
-
),
解得k2=1,即k=±1.
| 2 |
| 2 |
∵e=
| c |
| a |
| ||
| 2 |
∴b2=a2-c2=1.
所以椭圆C:
| x2 |
| 2 |
(II)设A(x1,y1),B(x2,y2).
由直线l与椭圆C交于两点A,B,则
|

消去y得到(1+2k2)x2-2=0,则x1+x2=0,x1x2=-
| 2 |
| 1+2k2 |
∴|AB|=
(1+k2)(0+
|
|
点M(
| 2 |
|
| ||
|
则|GH|=2
|
显然,若点H也在线段AB上,则由对称性可知,直线y=kx就是y轴,矛盾.
∵|AG|=|BH|,∴|AB|=|GH|.
∴
| 8(1+k2) |
| 1+2k2 |
| 7 |
| 3 |
| 2k2 |
| 1+k2 |
解得k2=1,即k=±1.
点评:熟练掌握椭圆与圆的标准方程及其性质、直线与曲线相交问题转化为把直线l的方程与曲线的方程联立得到一元二次方程、利用根与系数的关系及弦长公式、垂径定理及半径、弦长的一半、弦心距三者之间的关系(
)2=R2-d2是解题的关键.
| |GH| |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•海淀区一模)在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=
(2013•海淀区一模)在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN= (2013•海淀区一模)在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又∠CAD=30°,PA=AB=4,点N在线段PB上,且
(2013•海淀区一模)在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又∠CAD=30°,PA=AB=4,点N在线段PB上,且