ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥ΒΊ“ΣΫ®‘λ“ΜΗω±Ώ≥ΛΈΣ2Θ®ΒΞΈΜΘΚ![]() Θ©ΒΡ’ΐΖΫ–Έ –Οώ–ίœ–ΙΪ‘Α
Θ©ΒΡ’ΐΖΫ–Έ –Οώ–ίœ–ΙΪ‘Α![]() Θ§ΫΪΤδ÷–ΒΡ«χ”ρ
Θ§ΫΪΤδ÷–ΒΡ«χ”ρ![]() ΩΣΆΎ≥…“ΜΗω≥ΊΧΝΘ§»γΆΦΫ®ΝΔΤΫΟφ÷±Ϋ«Ήχ±ξœΒΚσΘ§Βψ
ΩΣΆΎ≥…“ΜΗω≥ΊΧΝΘ§»γΆΦΫ®ΝΔΤΫΟφ÷±Ϋ«Ήχ±ξœΒΚσΘ§Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§«ζœΏ
Θ§«ζœΏ![]() «Κ· ΐ
«Κ· ΐ![]() ΆΦœώΒΡ“Μ≤ΩΖ÷Θ§Ιΐ±Ώ
ΆΦœώΒΡ“Μ≤ΩΖ÷Θ§Ιΐ±Ώ![]() …œ“ΜΒψ
…œ“ΜΒψ![]() ‘Ύ«χ”ρ
‘Ύ«χ”ρ![]() ΡΎΉς“Μ¥ΈΚ· ΐ
ΡΎΉς“Μ¥ΈΚ· ΐ![]() Θ®
Θ®![]() Θ©ΒΡΆΦœώΘ§”κœΏΕΈ
Θ©ΒΡΆΦœώΘ§”κœΏΕΈ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ®Βψ
Θ®Βψ![]() ≤Μ”κΒψ
≤Μ”κΒψ![]() ÷ΊΚœΘ©Θ§«“œΏΕΈ
÷ΊΚœΘ©Θ§«“œΏΕΈ![]() ”κ«ζœΏ
”κ«ζœΏ![]() ”–«“÷Μ”–“ΜΗωΙΪΙ≤Βψ
”–«“÷Μ”–“ΜΗωΙΪΙ≤Βψ![]() Θ§ΥΡ±Ώ–Έ
Θ§ΥΡ±Ώ–Έ![]() ΈΣ¬ΧΜ·ΖγΨΑ«χ.
ΈΣ¬ΧΜ·ΖγΨΑ«χ.
Θ®1Θ©«σ÷ΛΘΚ![]() ΘΜ
ΘΜ
Θ®2Θ©…ηΒψ![]() ΒΡΚαΉχ±ξΈΣ
ΒΡΚαΉχ±ξΈΣ![]() Θ§
Θ§
ΔΌ”Ο![]() ±μ Ψ
±μ Ψ![]() ΓΔ
ΓΔ![]() ΝΫΒψΒΡΉχ±ξΘΜ
ΝΫΒψΒΡΉχ±ξΘΜ
ΔΎΫΪΥΡ±Ώ–Έ![]() ΒΡΟφΜΐ
ΒΡΟφΜΐ![]() ±μ Ψ≥…ΙΊ”Ύ
±μ Ψ≥…ΙΊ”Ύ![]() ΒΡΚ· ΐ
ΒΡΚ· ΐ![]() Θ§≤Δ«σ
Θ§≤Δ«σ![]() ΒΡΉν¥σ÷Β.
ΒΡΉν¥σ÷Β.
ΓΨ¥πΑΗΓΩΘ®1Θ©ΦϊΫβΈωΘ®2Θ©ΔΌMΘ®![]() Θ§0Θ©Θ§NΘ®
Θ§0Θ©Θ§NΘ®![]() Θ§2Θ©ΔΎSΘΫ4©¹Θ®t
Θ§2Θ©ΔΎSΘΫ4©¹Θ®t![]() Θ©Θ§Τδ÷–0ΘΦtΘΦ1Θ§SΒΡΉν¥σ÷Β «4
Θ©Θ§Τδ÷–0ΘΦtΘΦ1Θ§SΒΡΉν¥σ÷Β «4![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
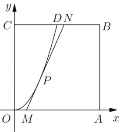
Θ®1Θ©ΗυΨίΚ· ΐyΘΫax2ΙΐΒψDΘ§«σ≥ωΫβΈω ΫyΘΫ2x2ΘΜ
”…![]() œϊ»ΞyΘ§άϊ”ΟΓςΘΫ0÷ΛΟςΫα¬έ≥…ΝΔΘΜ
œϊ»ΞyΘ§άϊ”ΟΓςΘΫ0÷ΛΟςΫα¬έ≥…ΝΔΘΜ
Θ®2Θ©ΔΌ–¥≥ωΒψPΒΡΉχ±ξΘ®tΘ§2t2Θ©Θ§¥ζ»κ÷±œΏMNΒΡΖΫ≥ΧΘ§”Οt±μ Ψ≥ω÷±œΏΖΫ≥ΧΘ§
άϊ”Ο÷±œΏΖΫ≥Χ«σ≥ωMΓΔNΒΡΉχ±ξΘΜ
ΔΎΫΪΥΡ±Ώ–ΈMABNΒΡΟφΜΐS±μ Ψ≥…ΙΊ”ΎtΒΡΚ· ΐSΘ®tΘ©Θ§
άϊ”ΟΜυ±Ψ≤ΜΒ» ΫΦ¥Ω…«σ≥ωSΒΡΉν¥σ÷ΒΘ°
Θ®1Θ©Κ· ΐyΘΫax2ΙΐΒψDΘ®1Θ§2Θ©Θ§
¥ζ»κΦΤΥψΒΟaΘΫ2Θ§
ΓύyΘΫ2x2ΘΜ
”…![]() Θ§œϊ»ΞyΒΟ2x2©¹kx©¹bΘΫ0Θ§
Θ§œϊ»ΞyΒΟ2x2©¹kx©¹bΘΫ0Θ§
”…œΏΕΈMN”κ«ζœΏOD”–«“÷Μ”–“ΜΗωΙΪΙ≤ΒψPΘ§
ΒΟΓςΘΫΘ®©¹kΘ©2©¹4ΓΝ2ΓΝbΘΫ0Θ§
ΫβΒΟb![]() ΘΜ
ΘΜ
Θ®2Θ©…ηΒψPΒΡΚαΉχ±ξΈΣtΘ§‘ρ0ΘΦtΘΦ1Θ§
ΓύΒψPΘ®tΘ§2t2Θ©ΘΜ
ΔΌ÷±œΏMNΒΡΖΫ≥ΧΈΣyΘΫkx+bΘ§
Φ¥yΘΫkx![]() ΙΐΒψPΘ§
ΙΐΒψPΘ§
Γύkt![]() 2t2Θ§
2t2Θ§
ΫβΒΟkΘΫ4tΘΜ
yΘΫ4tx©¹2t2
ΝνyΘΫ0Θ§ΫβΒΟx![]() Θ§ΓύMΘ®
Θ§ΓύMΘ®![]() Θ§0Θ©ΘΜ
Θ§0Θ©ΘΜ
ΝνyΘΫ2Θ§ΫβΒΟx![]() Θ§ΓύNΘ®
Θ§ΓύNΘ®![]() Θ§2Θ©ΘΜ
Θ§2Θ©ΘΜ
ΔΎΫΪΥΡ±Ώ–ΈMABNΒΡΟφΜΐS±μ Ψ≥…ΙΊ”ΎtΒΡΚ· ΐΈΣ
SΘΫSΘ®tΘ©ΘΫ2ΓΝ2![]() 2ΓΝ[
2ΓΝ[![]() Θ®
Θ®![]() Θ©]ΘΫ4©¹Θ®t
Θ©]ΘΫ4©¹Θ®t![]() Θ©Θ§Τδ÷–0ΘΦtΘΦ1ΘΜ
Θ©Θ§Τδ÷–0ΘΦtΘΦ1ΘΜ
”…t![]() 2
2![]() Θ§Β±«“ΫωΒ±t
Θ§Β±«“ΫωΒ±t![]() Θ§Φ¥t
Θ§Φ¥t![]() ±ΓΑΘΫΓ±≥…ΝΔΘ§
±ΓΑΘΫΓ±≥…ΝΔΘ§
Υυ“‘SΓή4![]() ΘΜΦ¥SΒΡΉν¥σ÷Β «4
ΘΜΦ¥SΒΡΉν¥σ÷Β «4![]() Θ°
Θ°

 ΩΦ«Α±ΊΝΖœΒΝ–¥πΑΗ
ΩΦ«Α±ΊΝΖœΒΝ–¥πΑΗ