题目内容
13．已知定义在R上的函数f（x）的导函数为f′（x），f（x）的极大值为f（1），极小值为f（-1），则函数y=（1-x）f′（x）的图象有可能是（ ）| A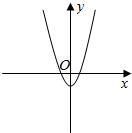． |  | B． |  | C． |  | D． |  |
分析 先求出函数f′（x）的符号，从而求出y=（1-x）f′（x）的符号，从而得到答案．
解答 解：∵f（x）的极大值为f（1），极小值为f（-1），
∴在（-∞，-1）上f′（x）＜0，在（-1，1）上f′（x）＞0，在（1，+∞）上f′（x）＜0，
①在（-∞，-1）上，1-x＞0，f′（x）＜0，
∴y=（1-x）f′（x）＜0，
②在（-1，1）上，1-x＞0，f′（x）＞0，
∴y=（1-x）f′（x）＞0，
③在（1，+∞）上，1-x＜0，f′（x）＜0，
∴y=（1-x）f′（x）＞0，
故选：C．
点评 本题考查了函数的单调性问题，考查导数的应用，是一道基础题．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
1．若π＜a＜2π，cos（a-7π）=-$\frac{3}{5}$，则sin（3π+a）•tan（a-$\frac{7}{2}$π）的值为（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{5}{4}$ | C． | $\frac{3}{5}$ | D． | $\frac{5}{3}$ |
5．函数f（x）在R上是增函数，若a+b≤0，则有（ ）
| A． | f（a）+f（b）≤-f（a）-f（b） | B． | f（a）+f（b）≥-f（a）-f（b） | C． | f（a）+f（b）≤f（-a）+f（-b） | D． | f（a）+f（b）≥f（-a）+f（-b） |