题目内容

已知点A（1，0），B（2，0）．若动点M满足
AB
•
BM
+
2
|
AM
|=0，则点M的轨迹方程为______．
设M的坐标为（x，y），可得
AM
=（x-1，y），
AB
=（1，0），
BM
=（x-2，y）
∴
AB
•
BM
=1×（x-2）+0×y=x-2，
|AM|
=
(x-1)2+y2

∵动点M满足
AB
•
BM
+
2
|
AM
|=0，
∴（x-2）+
2
•
(x-1)2+y2
=0
移项，平方得（x-2）2=2[（x-1）2+y2]
整理，得x2+2y2=2，
所以点M的轨迹方程为：
x2
2
+y2=1．
故答案为：
x2
2
+y2=1
练习册系列答案
相关题目
在⊿ABC中，设，，，
（1）若⊿ABC为正三角形，求证：；
（2）若成立，⊿ABC是否为正三角形.
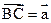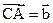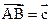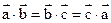若为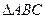的内心，且满足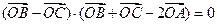，则
的形状为（    ）
A．等腰三角形B．正三角形C．直角三角形D．钝角三角形
已知在□ABCD中，点A（1，1），B（2，3），CD的中点为E（4，1），将
□ABCD按向量a平移，使C点移到原点O.
（1）求向量a；
（2）求平移后的平行四边形的四个顶点的坐标.
已知P是△ABC所在平面外一点，D是PC的中点，若
BD
=x
AB
+y
AC
+z
AP
，则x+y+z=（　　）
A．-1B．0C．
1
2
D．1
已知角α∈(0，π)，向量
m
=(2，-1+cosα)，
n
=(-1，cos2α)，
m
∥
n
，f(x)=sinx+
3
cosx
（Ⅰ）求角α的大小；
（Ⅱ）求函数f（x+α）的最小正周期与单调递减区间．
已知两定点M（4，0），N（1，0），动点P满足|
PM
|=2|
PN
|．
（1）求动点P的轨迹C的方程；
（2）若点G（a，0）是轨迹C内部一点，过点G的直线l交轨迹C于A、B两点，令f(a)=
GA
•
GB
，求f（a）的取值范围．
已知平面向量
α
，
β
(
α
≠
β
，
β
≠0）满足|
α
|=1，（1）当|
α
-
β
|=|
α
+
β
|=2时，求|
β
|的值；（2）当
β
与
α
-
β
的夹角为120°时，求|
β
|的取值范围．
已知抛物线C的顶点为坐标原点，焦点在x轴上，直线y＝x与抛物线C交于A，B两点，若P(2,2)为AB的中点，则抛物线C的方程为________．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网