Question

【题目】正方体ABCD﹣A1B1C1D1中，点M，N分别在线段AB1、BC1上，且AM=BN．以下结论：①AA1⊥MN；②A1C1∥MN；③MN∥平面A1B1C1D1；④MN与A1C1异面，⑤MN与 A1C1成30°．其中有可能成立的结论的个数为（ ）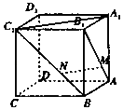
A.5
B.4
C.3
D.2

Answer 1

【答案】A
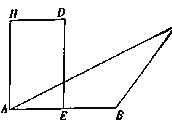
【解析】解：①作NE⊥BC，MF⊥AB，垂足分别为E，F，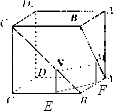
∵AM=BN，∴NE=MF，∴四边形MNEF是矩形，
∴MN∥FE，∵AA1⊥面AC，EF面AC，∴AA1⊥EF，∴AA1⊥MN，故①正确；
由①知，MN∥面AC，面AC∥平面A1B1C1D1 ， ∴MN∥平面A1B1C1D1 ，
故③正确；
MN∥FE，FE与AC所在直线相交时，MN与A1C1异面，FE与AC平行时，则平行，故②④可能成立；
⑤EF与AC成30°时，MN与 A1C1成30°．
故选A．
【考点精析】认真审题，首先需要了解棱柱的结构特征(两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形)．