题目内容
设a>b>0,则a2+ 的最小值是________.
的最小值是________.
4
【解析】a2+ =a2-ab+ab+
=a2-ab+ab+ =a(a-b)+
=a(a-b)+ +ab+
+ab+ ≥2+2=4.当且仅当a(a-b)=1且ab=1,即a=
≥2+2=4.当且仅当a(a-b)=1且ab=1,即a= ,b=
,b=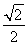 时取等号.
时取等号.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
题目内容
设a>b>0,则a2+ 的最小值是________.
的最小值是________.
4
【解析】a2+ =a2-ab+ab+
=a2-ab+ab+ =a(a-b)+
=a(a-b)+ +ab+
+ab+ ≥2+2=4.当且仅当a(a-b)=1且ab=1,即a=
≥2+2=4.当且仅当a(a-b)=1且ab=1,即a= ,b=
,b=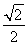 时取等号.
时取等号.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案