题目内容
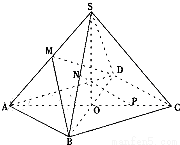
在正四棱锥S—ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC.
(1)指出动点P的轨迹(即说明动点P在满足给定的条件下运动时所形成的图形),证明你的结论;
(2)以轨迹上的动点P为顶点的三棱锥P-CDE的最大体积是正四棱锥S—ABCD体积的几分之几?
(3)设动点P在G点的位置时三棱锥P-CDE的体积取最大值V1,二面角G—DE—C的大小为α,二面角G—CE—D的大小为β,求tanα∶tanβ的值;
(4)若将“E是BC的中点”改为“E是BC上异于B、C的一定点”,其他条件不变,请指出点P的轨迹,证明你的结论.
解:(1)如图,分别取CD、SC的中点F、G,连结EF、EG、FG、BD.设AC与BD的交点为O,连结SO,则动点P的轨迹是△SCD的中位线FG.

由正四棱锥可得SB⊥AC,EF⊥AC.又∵EG∥SB,∴EG⊥AC,
∴AC⊥平面EFG,∵P∈FG,E∈平面EFG,
∴AC⊥PE.
(2)由于S△CDE是定值,所以当P到平面CDE的距离最大时,V P—CDE最大,易知当P与G重合时,P到平面CDE的距离最大,
故(VP—CDE) max=VG—CDE,又S△CDE=![]() S正方形ABCD,
S正方形ABCD,
G到平面ABCD的距离是点S到平面ABCD的距离的![]() ,
,
∴(VP—CDE) max=VG—CDE=![]() VS—ABCD.
VS—ABCD.
(3)令AB=a,EF与AC交于N点,连结GN,则GN⊥平面ABCD.因此二面角G—DE—C和二面角G—CE—D的平面角的正切值的比就等于N到DE和CE的距离的倒数比.
∵N是OC的中点,∴N到BC的距离为![]() a.
a.
连结DE交OC于M,则M是△DBC的重心,∴MN=![]() .
.
又ME=![]() a,NE=
a,NE=![]() ,
,
在Rt△MNE中,容易求得N到DE的距离为![]() .
.
故tanα∶tanβ=![]() ∶1.
∶1.
(4)动点P在侧面SCD内部及其边界上运动,且总保持PE⊥AC,那么这些相交于定点E的直线系应位于某个与直线AC垂直的平面内,而由正四棱锥的性质可知,AC⊥平面SBD,因此动直线PE集中在过E且平行于平面SBD的一个平面内.过E作EG′∥SB,EF′∥BD,分别交SC于G′,交CD于F′,则平面EF′G′∥平面SBD,从而AC⊥平面EF′G′,故点P的轨迹是线段F′G′.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案 如图,在正四棱锥S-ABCD中,AB=
如图,在正四棱锥S-ABCD中,AB= ,SA=10,M、N、O分别是SA、SB、BD的中点.
,SA=10,M、N、O分别是SA、SB、BD的中点.