题目内容
正三棱锥S-ABC的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,球心为O,M是线段SO的中点,过M与SO垂直的平面分别截三棱锥S-ABC和球所得平面图形的面积比为 .
【答案】分析:根据组合体的结构特征,得出截面三角形的面积S1= S△ABC=
S△ABC= ,再求出平面截球所得截面圆半径为
,再求出平面截球所得截面圆半径为 =
= 得出截面圆面积,再求比值即可.
得出截面圆面积,再求比值即可.
解答:解:由已知,△ABC是求大圆的内接正三角形,由于半径为1,所以边长AB= ,S△ABC=
,S△ABC= =
= .
.
因为M是线段SO的中点,且SO=1,所以平面截三棱锥S-ABC所得截面三角形的面积S1= S△ABC=
S△ABC=
平面截球所得截面圆半径为 =
= .截面圆面积S2=π×
.截面圆面积S2=π× =
= ,面积之比为
,面积之比为
故答案为: .
.
点评:本题考查球的内接几何体问题,考查分析、空间想象能力,转化计算能力.
 S△ABC=
S△ABC= ,再求出平面截球所得截面圆半径为
,再求出平面截球所得截面圆半径为 =
= 得出截面圆面积,再求比值即可.
得出截面圆面积,再求比值即可.解答:解:由已知,△ABC是求大圆的内接正三角形,由于半径为1,所以边长AB=
 ,S△ABC=
,S△ABC= =
= .
.因为M是线段SO的中点,且SO=1,所以平面截三棱锥S-ABC所得截面三角形的面积S1=
 S△ABC=
S△ABC=
平面截球所得截面圆半径为
 =
= .截面圆面积S2=π×
.截面圆面积S2=π× =
= ,面积之比为
,面积之比为
故答案为:
 .
.点评:本题考查球的内接几何体问题,考查分析、空间想象能力,转化计算能力.

练习册系列答案
相关题目
已知正三棱锥S-ABC的三条侧棱两两互相垂直,且SA=2
,则正三棱锥S-ABC的外接球的表面积是( )
| 3 |
| A、12π | B、32π |
| C、36π | D、48π |
 如图,正三棱锥S-ABC中,底面的边长是3,棱锥的侧面积等于底面积的2倍,M是BC的中点.
如图,正三棱锥S-ABC中,底面的边长是3,棱锥的侧面积等于底面积的2倍,M是BC的中点.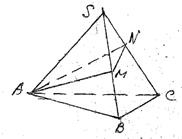 正三棱锥S-ABC的侧棱长为2,侧面等腰三角形的顶角为30°,过底面顶点作截面△AMN交侧棱SB、SC分别于M、N两点,则△AMN周长的最小值是
正三棱锥S-ABC的侧棱长为2,侧面等腰三角形的顶角为30°,过底面顶点作截面△AMN交侧棱SB、SC分别于M、N两点,则△AMN周长的最小值是
 如图正三棱锥S-ABC的侧棱与底面边长相等,如果E、F分别是SC、AB的中点,那么异面直线EF与SA所成的角为
如图正三棱锥S-ABC的侧棱与底面边长相等,如果E、F分别是SC、AB的中点,那么异面直线EF与SA所成的角为