题目内容
 如图,在正四棱锥S-ABCD中,AB=8
如图,在正四棱锥S-ABCD中,AB=8| 2 |
(1)设P是OC的中点,证明:PN∥平面BMD;
(2)求直线SO与平面BMD所成角的大小;
(3)在△ABC内是否存在一点G,使NG⊥平面BMD,若存在,求线段NG的长度;若不存在,说明理由.
分析:(1)建立空间坐标系,根据题意求出平面BMD的法向量
,因为
•
=0,进而得到线面平行.
(2)由(1)可得平面BMD的法向量,再求出直线OS所在的向量,利用向量之间的运算求出两个向量的夹角,再转化为线面角.
(3)若存在点G,设G点坐标为(x1,y1,0),结合题意可得:
∥
,即可求出点G的坐标,再检验点G的坐标满足题意,进而求出NG的长度.
| n |
| PN |
| n |
(2)由(1)可得平面BMD的法向量,再求出直线OS所在的向量,利用向量之间的运算求出两个向量的夹角,再转化为线面角.
(3)若存在点G,设G点坐标为(x1,y1,0),结合题意可得:
| n |
| NG |
解答:解:(1)以点O为原点,分别为OB、OC、OS所在直线为x轴、y轴、z轴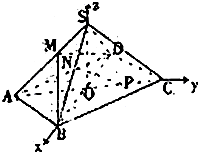 建立空间直角坐标系O-xyz,
建立空间直角坐标系O-xyz,
又因为
=(4,-4,3),
所以
•
=0,
又∵直线PN不在平面BMD内
∴PN∥平面BMD. …(4分)
(2)设直线SO与平面BMD所成角为θ,
所以sinθ=
=
=
,
∵θ∈(0,
)∴θ=arcsin
.…(8分)
(3)若存在点G,设G点坐标为(x1,y1,0),
所以点G坐标为(4,-
,0)…(10分)
在平面直角坐标系xoy中,△ABC的内部区域可表示不等式组:
,
经检验点G的坐标满足上述不等式组.
故在△ABC内存在一点G,使NG⊥平面BMD,且NG=
…(12分)
 建立空间直角坐标系O-xyz,
建立空间直角坐标系O-xyz,
|
又因为
| PN |
所以
| PN |
| n |
又∵直线PN不在平面BMD内
∴PN∥平面BMD. …(4分)
(2)设直线SO与平面BMD所成角为θ,
所以sinθ=
|
| ||||
|
|
| 24 |
| 6×5 |
| 4 |
| 5 |
∵θ∈(0,
| π |
| 2 |
| 4 |
| 5 |
(3)若存在点G,设G点坐标为(x1,y1,0),
|
所以点G坐标为(4,-
| 9 |
| 4 |
在平面直角坐标系xoy中,△ABC的内部区域可表示不等式组:
|
经检验点G的坐标满足上述不等式组.
|
故在△ABC内存在一点G,使NG⊥平面BMD,且NG=
| 15 |
| 4 |
点评:本题考查的知识点是直线与平面所成的角,直线与平面平行的判定以及直线与平面垂直的判定,夹角此类问题的关键是熟练掌握直线与平面夹角的定义,及空间线线、线面垂直关系之间的互相转化,或者建立空间直角坐标系利用空间向量的有关知识解决问题.

练习册系列答案
相关题目
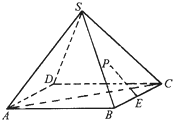 如图,在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC.则动点P的轨迹与△SCD组成的相关图形是( )
如图,在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC.则动点P的轨迹与△SCD组成的相关图形是( ) 如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论中恒成立的个数为( )
如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论中恒成立的个数为( ) 如图,在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC.则动点P的轨迹与△SCD组成的相关图形是( )
如图,在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC.则动点P的轨迹与△SCD组成的相关图形是( )
 如图,在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC.则动点P的轨迹与△SCD组成的相关图形是( )
如图,在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC.则动点P的轨迹与△SCD组成的相关图形是( )