题目内容
19.已知函数f(x)=log3x,x∈[3,27],g(x)=f2(x)-2m•f(x)+3的最小值为h(m).(1)求h(m);
(2)是否存在实数a,b,同时满足下列条件:
①b<a<1
②当h(m)的定义域为[b,a]时,值域为[b2,a2],若存在,求出a和b的值;若不存在,说明理由.
分析 (1)求出函数f(x)的值域,利用换元法把函数g(x)化为二次函数,求出它在闭区间上的最小值h(m)即可;
(2)根据题意得b<a<1时,h(m)在[b,a]上为减函数,求出h(m)在[b,a]上的值域,判断它是否满足题目中的条件即可.
解答 解:(1)∵函数f(x)=log3x,x∈[3,27],
∴1=log33≤f(x)≤log327=3,
即f(x)∈[1,3];
设f(x)=t,则t∈[1,3],
∴函数g(x)=f2(x)-2m•f(x)+3可化为
g(t)=t2-2mt+3=(t-m)2-m2+3,t∈[1,3];
当m≤1时,g(t)在[1,3]上是增函数,最小值是h(1)=4-2m;
当m≥3时,g(t)在[1,3]上是减函数,最小值是h(3)=12-6m;
当1<m<3时,g(t)在[1,3]上先减后增,最小值是h(m)=3-m2;
∴函数g(x)的最小值是h(m)=$\left\{\begin{array}{l}{4-2m,m≤1}\\{3{-m}^{2},1<m<3}\\{12-6m.m≥3}\end{array}\right.$;
(2)当m≤1时,h(m)=4-2m,
∴b<a<1时,h(m)在[b,a]上为减函数,
∴h(m)在[b,a]上的值域为[h(a),h(b)];
由题意,得$\left\{\begin{array}{l}{h(a){=b}^{2}}\\{h(b){=a}^{2}}\end{array}\right.$,即$\left\{\begin{array}{l}{4-2a{=b}^{2}}\\{4-2b{=a}^{2}}\end{array}\right.$,
两式相减,得2b-2a=b2-a2;
又a≠b,∴a+b=2,这与b<a<1矛盾;
∴不存在满足题中条件的a,b的值.
点评 本题考查了一次、二次函数的值域问题,也考查了换元法与转化思想的应用问题,对于二次函数在定区间上的值域问题一般结合图象和单调性来处理,是综合性题目.

| A. | 0 | B. | ∅ | C. | {0} | D. | {-1,0,1} |
| A. | (-∞,-2)∪(0,2) | B. | (-∞,-2)∪(2,+∞) | C. | (-2,0)∪(0,2) | D. | (-2,0)∪(2,+∞) |
 在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,点E在棱AC上,且BE⊥AC.
在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,点E在棱AC上,且BE⊥AC.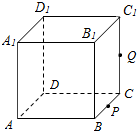 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则当CQ∈(0,$\frac{1}{2}$]∪{1}时,S为四边形;当CQ=$\frac{1}{2}$时S为等腰梯形;当CQ=1时,S的面积为$\frac{\sqrt{6}}{2}$.
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则当CQ∈(0,$\frac{1}{2}$]∪{1}时,S为四边形;当CQ=$\frac{1}{2}$时S为等腰梯形;当CQ=1时,S的面积为$\frac{\sqrt{6}}{2}$.