题目内容
4.如图1,在直角梯形PBCD中,DC∥PB,A为PB上一点,且ABCD为正方形,AC、BD相交于点E,沿AD将△PAD折起,使平面PAD⊥平面ABCD,连接PB、PC得四棱锥P-ABCD,如图2所示,F是PC的中点,G为AC上一动点.
(1)求证:BD⊥FG;
(2)若点G为线段EC中点,证明:FG∥平面PBD;
(3)若PA=AB=2,求三棱锥B-CDF的体积.
分析 (1)由已知条件,利用直线垂直于平面的判定定理,先推导出BD⊥平面APC,由此能够证明BD⊥FG.
(2)根据题设条件,利用直线与平面平行的判定定理进行证明.
(3)三棱锥B-CDF的体积等于三棱锥F-BCD的体积,利用等积法能求出结果.
解答 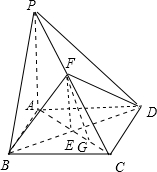 (1)证明:∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PA⊥AD,
(1)证明:∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PA⊥AD,
∴PA⊥平面ABCD,
∵BD?平面ABCD,
∴PA⊥BD,
∵ABCD为正方形,
∴BD⊥AC,
∵PA∩AC=A,
∴BD⊥平面PAC,
∵FG?平面PAC,
∴BD⊥FG;
(2)证明:连结PE,由F为PC中点,G为EC中点,知FG∥PE
而FG?平面PBD,PB?平面PBD,
故FG∥平面PBD;
(3)解:连结FE,FD,
∵F是PC中点,E是正方形ABCD对角线的交点,
∴FE∥PA,且FE=$\frac{1}{2}$PA=1,
∵PD⊥面ABCD,∴FE⊥面BCD,
∵S△BCD=$\frac{1}{2}×2×2$=2,
∴三棱锥B-CDF的体积V=VF-BCD=$\frac{1}{3}×1×2$=$\frac{2}{3}$.
点评 本题考查直线与直线垂直的证明,考查空间点位置的确定,考查三棱锥体积的求法,考查空间想象能力,逻辑思维能力,是中档题.解题时要注意空间思维能力的培养,注意等积法的合理运用.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
15.已知函数f(x)=$\frac{1}{|x|}$,g(x)=$\frac{x+|x-1|}{2}$,若f(x)<g(x),则实数x的取值范围是( )
| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-2)∪($\frac{1+\sqrt{17}}{4}$,+∞) | C. | (-2,$\frac{1+\sqrt{17}}{4}$) | D. | (-∞,-2)∪(1,2) |
9.某几何体的三视图如图所示,且该几何体的所有棱中,则该几何体的所有棱中,最长的棱为( )
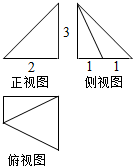

| A. | $\sqrt{14}$ | B. | $\sqrt{13}$ | C. | $\sqrt{5}$ | D. | 4 |


 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$. 如图,已知椭圆:$\frac{{x}^{2}}{4}$+y2=1,点A,B是它的两个顶点,过原点且斜率为k的直线l与线段AB相交于点D,且与椭圆相交于E、F两点.
如图,已知椭圆:$\frac{{x}^{2}}{4}$+y2=1,点A,B是它的两个顶点,过原点且斜率为k的直线l与线段AB相交于点D,且与椭圆相交于E、F两点.