题目内容
设函数f(x)=loga(1-(1)证明f(x)是(a,+∞)上的减函数;
(2)解不等式f(x)>1.
(1)证明:任取x1、x2∈(a+∞),且x1<x2,则f(x1)-f(x2)=loga(1-![]() )-loga(1-
)-loga(1-![]() )=loga
)=loga![]() .
.
∵![]() -1=
-1=![]() ,
,
∵0<a<1,a<x1<x2,
∴![]() >0,且
>0,且![]() -1<0,
-1<0,
即0<![]() <1,
<1,
∴loga![]() >0.
>0.
∴f(x1)>f(x2),∴f(x)是(a,+∞)上的减函数.
(2)解析:解法一:∵0<a<1,
∴f(x)>1![]() loga(1-
loga(1-![]() )>logaa
)>logaa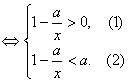
解不等式①得,x>a或x<0.
解不等式②得,0<x<![]() .
.
∵0<a<1,∴a<![]() ,
,
∴原不等式解集为{x|a<x<![]() }.
}.
解法二:函数f(x)的定义域为{x|x>a或x<0}.
∵0<a<1,
∴当x<0时,1-![]() >1.
>1.
∴f(x)=loga(1-![]() )<0,不合题意.
)<0,不合题意.
当x>a时,解方程f(x)=1,得x=![]() .
.
由(1)知f(x)是(a,+∞)上的减函数,
∴f(x)>1时,x<![]() .
.
∵a<![]() ,
,
∴原不等式解集为{x|a<x<![]() }.
}.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目