题目内容
10.若函数f(x)=loga(|x|-1)(a>0,a≠1)在区间(1,2)内恒有f(x)>0.则f(x)的单调递减区间为(1,+∞).分析 根据f(x)在区间(1,2)内恒有f(x)>0得出a的取值范围,再利用复合函数的单调性即可求出.
解答 解:由f(x)有意义得:
|x|-1>0,
解得:x<-1或x>1.
令g(x)=|x|-1,则g(x)在(-∞,-1)上递减,在(1,+∞)上递增.
当x∈(1,2)时,|x|-1∈(0,1).
∵函数f(x)=loga(|x|-1)(a>0,a≠1)在区间(1,2)内恒有f(x)>0,
∴0<a<1.
∴f(x)的单调递减区间为(1,+∞).
点评 本题主要考查了对数函数的定义域,复合函数的单调性.属于中档题.

练习册系列答案
相关题目
18.若关于x的方程(log2x)2+2alog2x+1=0有大于1的实数解,则实数a的取值范围是( )
| A. | (-∞,-1] | B. | [1,+∞) | C. | (1,+∞) | D. | (-∞,-1]∪[1,+∞) |
5.已知等差数列{an}的前n项和为Sn,且满足a1=9,S5=35,则使Sn取最大值的n的值为( )
| A. | 8 | B. | 10 | C. | 9或10 | D. | 8和9 |
15.不等式2+log0.5(5-x)+log2$\frac{1}{x}$>0的解集是( )
| A. | (0,+∞) | B. | (-∞,5) | C. | (0,1)∪(4,5) | D. | 空集 |
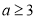 ,函数
,函数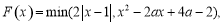 其中
其中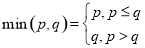 .
. 成立的
成立的 的取值范围;
的取值范围; 的最小值
的最小值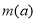 ;
;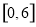 上的最大值
上的最大值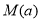 .
. 中,侧面
中,侧面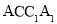 与侧面
与侧面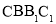 都是菱形,
都是菱形, ,
, .
.
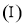 求证:
求证: ;
; 若
若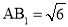 ,求二面角
,求二面角 的余弦值.
的余弦值.