题目内容
求在两坐标轴上截距相等,且与点A(3,1)的距离为2的直线方程.
所求直线方程为x-y=0,x+7y=0, x+y-2=0,x+y-6="0."
(1)当直线过原点时,设直线方程为y=kx,
即kx-y=0.
由题设得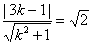 ,
,
解得k=1或 .
.
∴所求直线的方程为x-y=0或x+7y=0.
(2)当直线不经过原点时,设所求直线的方程为 即x+y-a=0.
即x+y-a=0.
由题意,有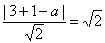 ,解得a=2或a=6.
,解得a=2或a=6.
∴所求直线的方程为x+y-2=0或x+y-6=0.
综上,知所求直线方程为x-y=0,x+7y=0, x+y-2=0,x+y-6=0.
即kx-y=0.
由题设得
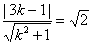 ,
,解得k=1或
 .
.∴所求直线的方程为x-y=0或x+7y=0.
(2)当直线不经过原点时,设所求直线的方程为
 即x+y-a=0.
即x+y-a=0.由题意,有
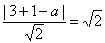 ,解得a=2或a=6.
,解得a=2或a=6.∴所求直线的方程为x+y-2=0或x+y-6=0.
综上,知所求直线方程为x-y=0,x+7y=0, x+y-2=0,x+y-6=0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
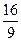 π (B)
π (B)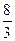 π (C)4π (D)
π (C)4π (D) π
π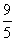 B.
B.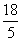 C.3 D.6
C.3 D.6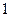 的正四面体内有一点
的正四面体内有一点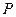 ,由点
,由点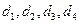 ,则
,则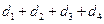 的值为 。
的值为 。