题目内容
函数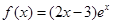 的单调递增区间是( )
的单调递增区间是( )
A.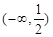 | B.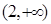 | C. | D.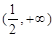 |
D
解析试题分析: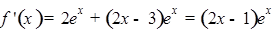 ,单调递增区间有,
,单调递增区间有,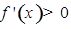 ,可得
,可得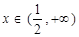 .
.
考点:由导数求函数的单调性.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
已知 是R上的单调增函数,则
是R上的单调增函数,则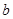 的取值范围是( )
的取值范围是( )
A.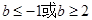 | B.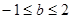 | C.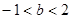 | D.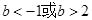 |
设函数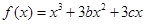 有两个极值点
有两个极值点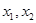 ,且
,且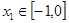 ,
,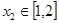 ,则( )
,则( )
A. | B.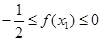 |
C. | D.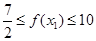 |
等比数列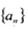 中,
中,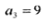 前三项和为
前三项和为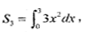 ,则公比q的值是( )
,则公比q的值是( )
| A.1 | B.- | C.1或- | D.-1或- |
设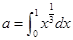 ,
,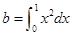 ,
,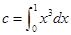 ,则
,则 的大小关系是( )
的大小关系是( )
A.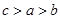 | B.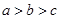 | C.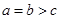 | D.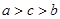 |
下列求导运算正确的是( )
A.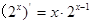 | B.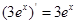 |
C.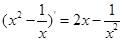 | D.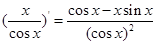 |
设函数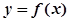 在
在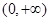 内有定义,对于给定的正数
内有定义,对于给定的正数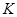 ,定义函数
,定义函数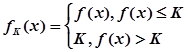 ,取函数
,取函数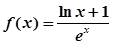 ,恒有
,恒有 ,则( )
,则( )
A.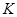 的最大值为 的最大值为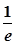 | B.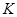 的最小值为 的最小值为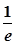 | C.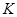 的最大值为2 的最大值为2 | D.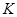 的最小值为2 的最小值为2 |
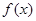 与
与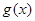 是定义在
是定义在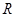 上的两个可导函数,若
上的两个可导函数,若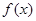 ,
,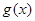 满足
满足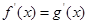 ,则
,则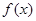 与
与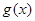 满足( )
满足( )
A.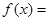 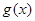 | B.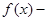 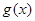 为常数函数 为常数函数 |
C.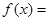 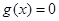 | D.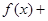 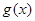 为常数函数 为常数函数 |
把一个周长为12cm的长方形围成一个圆柱,当圆柱的体积最大时,该圆柱底面周长与高的比为( )
| A.1:2 |
| B.1:π |
| C.2:1 |
| D.2:π |